с одним заданием по алгебре Найдите предел функции y = f(x) при x –> x0
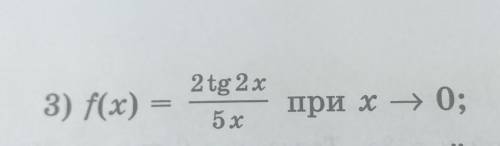
Другие вопросы по теме Алгебра
Популярные вопросы
- Найдите длину шестидесятой параллели Земли. Во сколько раз она длиннее...
1 - Нарисуйте многогранник: а) около которого можно описать сферу; б) около...
3 - Как построить: а) прямую, центрально-симметричную данной; б) плоскость,...
2 - Нарисуйте шар. а) Нарисуйте шар, центрально-симметричный данному относительно...
1 - Нарисуйте такие фигуры, которые имеют: а) центр симметрии; б) плоскость...
3 - Нарисуйте сечение шара. Нарисуйте сечение, симметричное ему относительно...
1 - Какой фигурой является сечение цилиндра плоскостью, параллельной его...
1 - Докажите, что около цилиндра можно описать сферу. Это означает, что...
3 - Говорят, что сфера вписана в цилиндр, если она касается его оснований,...
2 - Какой фигурой является проекция цилиндра на плоскость: а) параллельную...
2
4/5
Объяснение:
для решения данного примера необходимо знать одно из следствий первого замечательного предела:
lim (x→0) (tg x)/x = 1
3) lim (x→0) (2 tg 2x)/5x =
(используя следствие первого замечательного предела):
=lim (x→0) (2 * 2 tg 2x)/(5х*2)=
=lim (x→0) (2*2/5)* ( tg 2x)/2x =
= (2*2/5) * lim (x→0) ( tg 2x)/2x =
[ х→0, соответственно 2х→0]
= (2*2/5) * lim (2х→0) ( tg 2x)/2x =
= (2*2/5) * 1 = 4/5 * 1 = 4/5
( используя правило Лопиталя):
= lim (x→0) (2 tg 2x)' / (5x)' =
= lim (x→0) (2 * (2х)' * (1 / cos² 2x)) / 5 =
= lim (x→0) (2*2 / cos² 2x) / 5 =
= lim (x→0) (2*2/5) * ( 1/ cos² 2x) =
= (2*2/5) * lim (x→0) (1/cos²(2x)) =
= 4/5 * (1/cos²(2*0))=
= 4/5 * 1/1² = 4/5 * 1 = 4/5