С. нужно 1) 2) там 1/3 в степени x^2-7x+6
2) там 1/3 в степени x^2-7x+6 ^x^2-7x+6\leq 9^{x-1}) 3) система уравнений знак системы: 2^x умножить на 5^y=20 2^y умножить на 5^x=50
3) система уравнений знак системы: 2^x умножить на 5^y=20 2^y умножить на 5^x=50
Другие вопросы по теме Алгебра
Популярные вопросы
- В какую сторону врощветься земля...
3 - На копирование 99 страниц первый принтер тратит на 2 мин меньше,...
2 - Плот изготовлен из восьми сосновых досок длиной 4 м, толщиной 50...
3 - Классикалық әдіс дегеніміз не? ...
3 - Адамның өзі жасаған әдеби, драмалық және музыкалық шығармаларға,...
2 - 1. Оцените, какие из реформ М. Тэтчер положительно (+), а какие...
3 - 1.Engineers are developing a artificial / fake eye for the blind...
3 - ЖазылымОкылым материалының ғылыми фантастика екенін дәлелдейтін...
3 - сделать два последних примера, а точнее 3) и 4). Надо и прямо сейчас,...
1 - Плоскости граней двух выпуклых многогранников совпадают. Обязательно...
1
1)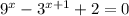
Введём новую переменную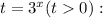
Корни квадратного уравнения t1=1, t2=2, подставляем:
2)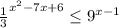
Приведём всё к общему основанию (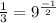
Функция возрастающая, то есть знак не меняется:
Решаем это уравнение методом интервалов (корни 4 и 1):
Промежутки будут следующие: x ∈ [-∞;1] ∪ [4; +∞].
3)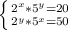
Ну, тут я наугад если честно отгадал 1 и 2 :)