С дифференциала приближенно вычислить данные величины
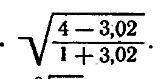
Другие вопросы по теме Алгебра
Популярные вопросы
- Казахстана) объяснить термин или понятие: 1) колониальный гнет - 2) национально...
1 - Впонедельник цена акции составляла 2 000 рублей., в среду она уменьшилась на 5...
1 - Разберите предложение: я хочу жить и работать в париже! (как что подчеркнуть? !...
2 - Критерий рейнольдса re = 10 000. какой режим движения жидкости в трубопроводе:...
1 - Задали по краеведенью командную работу надо придумать девиз. команда: совушки....
1 - Водном из канадских заповедников уничтожили всех волков чтобы добиться увеличения...
2 - Значение вырождения (sint-cost)^2+2*sint*cost равно:...
1 - Денис раскрасил в альбоме 4 страницы,это пятая часть всех страниц в альбоме.сколько...
2 - Выберите правильную видовременную форму и залог для глагола в скобках. all the...
2 - Вкорзине лежат чёрные и белые шары чёрные шары составляют 4/7 всего количество...
1
Введем функцию
надо вычислить значение функции в точке х= 3,02
Приближенные вычисления с дифференциала функции одной переменной:
х=x₀+Δx= 3+0.02
f(x₀+Δx)≈f(x₀)+f ` (x₀)*Δx
1. найдем f(x₀)
2. найдем производную
теперь найдем f ` (x₀)*Δx
3. и теперь найдем приближенное значение
f(x₀+Δx)≈f(x₀)+f ` (x₀)*Δx ≈ 1/2-0,00625≈0,5-0,00625≈0,49375