1. Алгебра
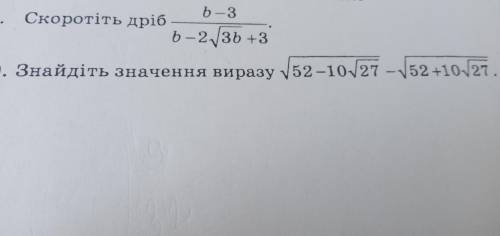
  2. с алгеброй,последнее задание

с алгеброй,последнее задание


с алгеброй,последнее задание

Zhenya12123 Zhenya12123    2   11.03.2021 13:58    0

Ответы
sharudakatya25oxzgq7 sharudakatya25oxzgq7  10.04.2021 13:59

\sqrt{52-10\sqrt{27} }-\sqrt{52+10\sqrt{27} }=-10

Объяснение:

Представим подкоренное выражение 52-10√27 в виде квадрата разности.

52-10\sqrt{27}=52-2\cdot5\cdot\sqrt{27}=25+27-2\cdot5\cdot\sqrt{27}=5^2-2\cdot5\cdot\sqrt{27}+(\sqrt{27})^2=(5-\sqrt{27})^2

Представим подкоренное выражение 52+10√27 в виде квадрата суммы.

52+10\sqrt{27}=52+2\cdot5\cdot\sqrt{27}=25+27+2\cdot5\cdot\sqrt{27}=5^2+2\cdot5\cdot\sqrt{27}+(\sqrt{27})^2=(5+\sqrt{27})^2

Подставим полученные выражения под корни

\sqrt{52-10\sqrt{27} }-\sqrt{52+10\sqrt{27} }=\sqrt{(5-\sqrt{27})^2 }-\sqrt{5+\sqrt{27})^2 }=|5-\sqrt{27}|-|5+\sqrt{27} |=\sqrt{27}-5-5-\sqrt{27}=-10

Подмодульное выражение 5-√27 меньше нуля поэтому раскрываем модуль с противоположным знаком |5-√27|=√27 -5

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
artyom11111112 artyom11111112  15.09.2019 20:20
С3 . cамое большое кол-во . срочо. 1. найти область определения функции а) y =√(2x - 5) б) y = 6/(x - 1) в) y = √( (x - 5) / (2x + 3) ) г) y = 2x / (х^2 - 5x + 6) 2. исследовать функции...
КириллАлек КириллАлек  15.09.2019 20:20
Постройте график функции у=|1-|х+3| | найти наименьшее и наибольшее...
karolinaanime karolinaanime  15.09.2019 20:20
Вычислите cos123° • cos 57°+ sin123° • sin 57°...
Gootya1 Gootya1  15.09.2019 19:03
Pешите сpочно 10 уpавнений х(в квадpате)-4х=0 х(в квадpате)-13х+3-=0 х(в квадpате)-5х+6=0 х(в квадpате)-8х=0 х(в квадpате)-х-6=0 х(в квадpате)+7х-30=0 х(в квадpате)+4х=0 х(в квадpате)+13х+42=0...
valeriy345 valeriy345  15.09.2019 19:03
Степень степени 2/5 в 3 степени ​...
Sodadus Sodadus  15.09.2019 19:04
Дослідити на парність приклади...
gamerallgames3457643 gamerallgames3457643  15.09.2019 19:04
Докажите что в уравнение х²+6х+10=0 нет корней...
tigranchik111111 tigranchik111111  15.09.2019 20:20
Вычислить с решением: 1) 2√22x2√3x√66 2)(√42-2)в степени2 3) -0,2x(-10)c степени2+53...
Папкинапапка222 Папкинапапка222  15.09.2019 20:20
На экзамене студенту предлагается 30 билетов , в каждом по три вопроса. из 90 вопросов, вошедших в билеты, студент знает 45. какова вероятность, что взятый студентом билет будет состоять...
gulia2369 gulia2369  15.09.2019 20:20
Докажите, что значение выражения 101^12-64^2 кратно 99 ^ - это степень...

Популярные вопросы