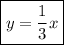с алгеброй...Нужно понятное и подробное решение. Найдите асимптоты графиков функций.
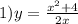
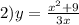
Другие вопросы по теме Алгебра
Популярные вопросы
- Стороны квадрата 10 см, найдите площадь квадрата...
1 - Одна бригада рабочих может исполнять определенную работу за 5 часов ,а вторую за...
1 - Можно ли замостить (без наложений и пробелов) доминошками 1×2 квадрат 5×5? (если...
1 - Вычислите с объяснением . 46*2 ; 5*18 ; 19*3 ; 4*17 ; 45 *2 ;...
1 - Подскажите как сочинить сочинение по этому плану. подскажите как сочинить сочинение...
1 - Какие показатели влияют на качество и перспективы разработки нефти(западно-сибирская...
3 - Есть ли место гераклу в современном мире?...
1 - Маленький рассказ о жизни земледельцев в египте...
2 - Придумать миф о любом славянском боге...
1 - Разобрать слово по составу --разнообразная, рассказывали...
2
1.
Вертикальная асимптота: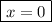 , так как в этой точке функция не определена, а предел
, так как в этой точке функция не определена, а предел 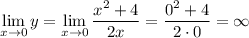 .
.
Наклонная асимптота: задается уравнением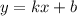 . Найдем коэффициенты:
. Найдем коэффициенты:
Наклонная асимптота: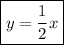
2.
Вертикальная асимптота: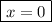 , так как в этой точке функция не определена, а предел
, так как в этой точке функция не определена, а предел 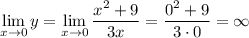 .
.
Наклонная асимптота: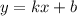
Наклонная асимптота: