с Алгеброй найти сумму корней уравнения
Другие вопросы по теме Алгебра
Популярные вопросы
- 4. дополнением aij элемента aij квадратной матри¬цы a называется: • минор этого...
2 - (1 5/6-1 3/4)*2,4 (-3/25+1 1/3)*7,5 (6,5-8 3/4): 1/8 (-2/9+3 1/18)*1,8 (-0,375+2...
3 - 4. глаголы с фиксированными предлогами. перепишите предложения, заполняя пропуски...
2 - Почему соединение ,при котором шуруп ввинчивается в основную деталь поперёк волокон...
3 - Поставьте следующие предложения в вопросительную и отрицательную форму. 1. when...
1 - Атмосферное давление (мм рт. ст.) москва - 750. в сторону какого города будет...
3 - Из слова motivation составить новые слова...
1 - Кто знает краткое содержание в.г.кароленко последний луч ? подскажите !...
1 - Нужны колядки про деньги(теп подайте денег и у вас в доме будет счастье)...
1 - Найдите значение выражения (3 2/3-1 2/7*5 4/9): (-2,5)...
2
Замена: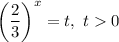
Обратная замена:
Сумма корней: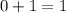
ответ: 1.
ответ: 3 ◀