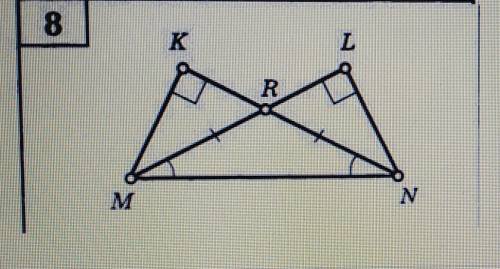
с алгеброй надо найти пары равных треугольников и доказать их равенство
Другие вопросы по теме Алгебра
Популярные вопросы
- Can you room before you go out,please...
3 - Определите личные местоимения как член предложения 1)я еще тогда был ребенок,...
2 - Найдите значение выражения: -5(2x+y)+1,5(3y-x), если x=10, y=1...
2 - Из какого произведения эти строки? кто их автор? и вот, когда силы покинули капитана...
2 - Вставь пропущенные числа сделай проверку _1541_3_ | 3_8 1_4_ | _1••• •••2 0 (3...
1 - Туристы отправились в путешествие. в первый день они проехали на велосипедах 43км345м,а...
1 - По матиматике за один маляр. за покраску получил 455 гривен а второй 325 гривен....
1 - Посажено 10 кустов чёрной смородины, что составляет 50% от числа посаженых кустов...
3 - Древнего казахстана 6 класс древний центр метолургии архитектура стиля рунические...
2 - Поставь скобки правильно 7*8+4/4+2=65 7*8+4/4+2=77...
1
Для начала, давайте обозначим вершины треугольников заглавными буквами, чтобы было проще говорить о них. Также помним, что стрелочка на стороне означает, что данная сторона равна указанной стороне у другого треугольника.
В задаче даны два треугольника: ABC и DEF.
Начнем сравнение. Посмотрим на стороны треугольников:
AB = DE (это указано на диаграмме)
AC = DF (это указано на диаграмме)
BC = EF (это указано на диаграмме)
Теперь перейдем к углам треугольников:
< A = < D (это указано на диаграмме)
< B = < E (это указано на диаграмме)
< C = < F (это указано на диаграмме)
Мы видим, что все стороны и углы одного треугольника соответствуют сторонам и углам другого треугольника. Исходя из этого, мы можем сделать вывод, что треугольники ABC и DEF равны друг другу.
Доказательство такого равенства основывается на конгруэнтности треугольников, то есть на равенстве соответствующих сторон и углов.
Надеюсь, что ответ был понятен и помог вам разобраться в задаче. Если у вас остались вопросы, не стесняйтесь задавать их."