1. Алгебра
  2. Розвзати задачу , склавши

Розвзати задачу , склавши систему рівнянь: Знайти дріб, який дорівнює 34, якщо його чисельник збільшити на 6, і який дорівнює 12, якщо його знаменник зменшити на 2.

roldugina78 roldugina78    3   30.05.2023 08:00    0

Ответы
Biserka1999 Biserka1999  30.05.2023 08:01

Відповідь:

дріб -   \dfrac{9}{20}

Пояснення:

Уточненна умова: Знайти дріб, який дорівнює 3/4, якщо його чисельник збільшити на 6, і який дорівнює 1/2, якщо його знаменник зменшити на 2.

Розвязання:

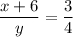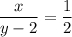Нехай чисельник дробу дорівнює x, знаменник дробу - у, тоді шуканий дріб  \dfrac{x}{y} . Після того, як чисел дробу збільшити на 6, то будемо отримувати дріб рівний \dfrac{3}{4}, тобто \dfrac{x+6}{y}=\dfrac{3}{4}.  А якщо знаменник зменшити на 2, то будемо отримувати дріб рівний \dfrac{1}{2}, тобто \dfrac{x}{y-2} =\dfrac{1}{2} . Складемо рівняння:

\left \{ \begin{array}{ccc} \dfrac{x+6}{y}=\dfrac{3}{4}, \dfrac{x}{y-2}=\dfrac{1}{2}; \end{array}\right

\begin{cases}4(x+6)=3y \hspace{1.2em}\\2x=y-2 \hspace{1.2em}\end{cases}

\begin{cases}4x+24=3y \hspace{1.2em}\\2x+2=y \hspace{1.2em}\big | \cdot (-3)\end{cases}

\begin{array}{r} \underline {+ \begin{cases}4x+24=3y \hspace{1.2em}\\-6x-6=-3y \hspace{1.2em}\end{cases} \end{array} } \\ \begin{array}{r} \quad\quad-2x+18=0 \\ \begin{array}{r} \quad\quad-2x=-18 \end{array} \end{array}\\

\qquad \quad \begin{array}{r} \quad\quad x=\dfrac{-18}{-2} \end{array} \end{array} \\

x=9

\begin{cases} x=9 \hspace{1.2em}\\y=2x+2 \hspace{1.2em}\end{cases}

\begin{cases} x=9 \hspace{1.2em}\\y=2\cdot9+2 \hspace{1.2em}\end{cases}

\begin{cases} x=9 \hspace{1.2em}\\y=20 \hspace{1.2em}\end{cases}

Отже, чисельник дробу 9, знаменник 20, а шуканий дріб \dfrac{9}{20}.

Відповідь: дріб -   \dfrac{9}{20}.

#SPJ1

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
damiramirov321 damiramirov321  14.06.2019 11:10
У=2х^2+8х+2 квадратичная функция графиком является парабола,ветви которой направлены вверх т.к а=2,а 0. (постройте параболу)...
jula1985ozpajo jula1985ozpajo  14.06.2019 11:10
Какое число является решением системы неравенств 2x 15 3x+7 7...
ylianа06 ylianа06  14.06.2019 11:10
(а-в)(а+в) -(а-в)^2/ав-в^2 ответы а)-2/в^2 в)2/в^2 в)2 г) 2а б/а-в ....
Катюха123Печенька Катюха123Печенька  14.06.2019 11:10
4-а/а-3 +2а-5/3- а)а-1/а- б)3 в) -3 г)1-3а/а-3...
AsiyaEkb AsiyaEkb  14.06.2019 11:10
На строительство плотины укладчики бетона,перевыполняя дневную норму на 180м бетона,не только выполнили 10 дневное за 1 день до срока,но и уложили дополнительно 320м бетона.какова...
anchousuchixa anchousuchixa  26.11.2020 10:49
Розкласти на множники 7х-7у...
Айхан1111111 Айхан1111111  26.11.2020 10:49
Только те каторые Карандашом отмечены...
nizametdinovaalina nizametdinovaalina  26.11.2020 10:49
Найди числовое значение многочлена b×b+2by+y×yпри b=4 и y=−10.​...
EvaBagatelya EvaBagatelya  26.11.2020 10:49
Тема: Применение производной к решению задач....
kristinaabrosi1 kristinaabrosi1  05.09.2019 17:25
Не пролистывай ! , будь другом . два примера , по действием , с решением .(решение по действиям нужно ) . буду и 50 ( это на оценку ) ​...

Популярные вопросы