Розв'яжіть три окремі системи.
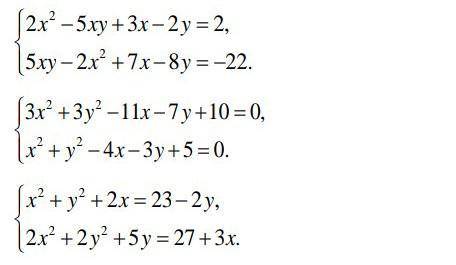
Другие вопросы по теме Алгебра
Популярные вопросы
- :с добра тому, кто решит 1. найдите площадь треугольника, стороны которого равны...
1 - Восновании прямой призмы лежит прямоугольный треугольник с катетами 5 и 12. боковые...
2 - Какое прилагательное нельзя просклонять? а) туманный б) сильна в) зелёный...
1 - Докажите что легенда об арионе это легенда...
2 - Изатем найдите значения выражения m+87+23 если m=39; m=196...
1 - Вычислите площадь квадрата со стороной a, равной 9.4...
1 - Напишите короткое сочинение рассуждение на тему надо ли заботиться и духовном здоровье?...
3 - 10 миллионов в счете назывались ещё и так...
3 - Среди 67 учащихся курсов иностранных языков в 47 человек изучают 35 a23 оба языка...
1 - Как решить этот пример –4(5c-2d)+5(4c-3d)...
2
сложения:
одно из уравнений системы заменим на сумму уравнений:
подстановки: выразим y из второго уравнения и подставляем в первое
D=9-8=1
О т в е т.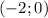 ;
; 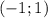
2)
чтобы применить сложения, умножаем второе уравнение на (-3)
сложения:
оставляем второе уравнение, а первое заменяем суммой двух уравнений:
подстановки: выразим x из второго уравнения и подставляем в первое
D=9-8=1
О т в е т.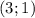 ;
; 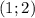
3)
умножаем первое уравнение на (-2)
сложения:
оставляем первое уравнение, а второе заменяем суммой двух уравнений:
подстановки: выразим y из второго уравнения и подставляем в первое
D=25+24=49
О т в е т.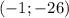 ;
; 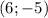
Розв'язання завдання додаю