1. Алгебра
  2. Розв’яжіть систему рівнянь:

Розв’яжіть систему рівнянь: (Решите систему уравнений:) 1/x-1/y=1/12
-y+2x=2

ответы без решения не принимаются! Заранее


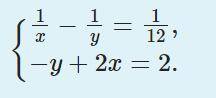
Розв’яжіть систему рівнянь: (Решите систему уравнений:) 1/x-1/y=1/12 -y+2x=2 ответы без решения не п

polina4673738 polina4673738    1   04.02.2021 03:19    0

Ответы
khokhr khokhr  04.02.2021 06:00

(x_1,\,y_1) = (4,\,6)\\(x_2,\,y_2) = (3,\,4)

Объяснение:

\begin{equation*}\left \{\begin{array}{l}\frac{1}{x} - \frac{1}{y} = \frac{1}{12}\\-y + 2x = 2 \end{array} \Leftrightarrow\left \{\begin{array}{l}\frac{1}{x} - \frac{1}{y} = \frac{1}{12}\\y = 2x - 2 \end{array}\Leftrightarrow\left \{\begin{array}{l}\frac{1}{x} - \frac{1}{2x-2} = \frac{1}{12}\\y = 2x - 2 \end{array}\right\right

Решаем первое уравнение:

\frac{1}{x} - \frac{1}{2x - 2 } = \frac{1}{12}\\\\\frac{2x - 2}{2x^2-2x} - \frac{x}{2x^2-2x} = \frac{1}{12}\\\\\frac{x - 2}{2x^2-2x} = \frac{1}{12} \\\\12x-24 = 2x^2-2x \\\\2x^2-14x+24 = 0\\\\x^2 - 7x +12 = 0 \\\\D = 7^2-4\cdot12 = 1 \\\\x_{1,2} = \frac{7 \pm 1}{2}, \ x_1 = 4, \ x_2 = 3

Подставляем полученные значения во второе уравнение и находим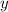 y:

\begin{equation*}\left \{\begin{array}{l}x_1 = 4\\y_1 = 2\cdot4 - 2 = 6 \end{array} \end{array} \\\\\\\begin{equation*}\left \{\begin{array}{l}x_2 = 3\\y_2 = 2\cdot3 - 2 = 4 \end{array} \end{array}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
polinavak05 polinavak05  12.03.2021 10:21
очень , 7 клас, если можно с розяснением...
катя5087 катя5087  12.03.2021 10:23
Решите 5 быстрее , а то сор идет. 5 задание надо...
папа336 папа336  06.03.2019 21:40
Выполнить указанные действия a²,8·4,a=?...
стланка стланка  06.03.2019 21:40
Автомобиль проехал 30км за х часов скорость велосепидиста в 3 раза меньше скорости автомобиля за какое время проедит велосепидист 90км?...
ivanovali0109 ivanovali0109  06.03.2019 21:40
Торт важить 4\5кг і ще 4\5 своєї ваги. скільки важить торт...
nikin25 nikin25  06.03.2019 21:40
От заречной до мухино я шёл 0,8ч со скоростью 5,5 км/ч , а от мухино до каменки ехал на велосипеде 1,4 ч со скоростью 12,5 км/ч . на сколько километров мухино дальше...
albina1002 albina1002  06.03.2019 21:40
На x грн купили книги.если на ети же деньги купят на 4 книги меньше то каждая книга будет дороже на 1 грн . сколько книг купили? (решается через систему уравнений-но...
hohotuchka hohotuchka  06.03.2019 21:50
Если длину прямоугольника уменьшить на 2 см, а ширину увеличить на 1 см, то получится квадрат, площадь которого на 4 квадратных сантиметра меньше площади прямоугольника....
kazybekabdrahman0707 kazybekabdrahman0707  06.03.2019 21:50
Найдите два натуральных числа,сумма которых равна 168,а наименьшее общее кратное равно 1001...
Анастасия8383 Анастасия8383  06.03.2019 21:50
3х в кубе - 2у в кубе - 6х в квадрате умножить у в квадрате + ху при х=две третьих и у= одна вторая...

Популярные вопросы