Розв'язати систему рівнянь: x2 +2xy+y2=1, x2 —xy = 6
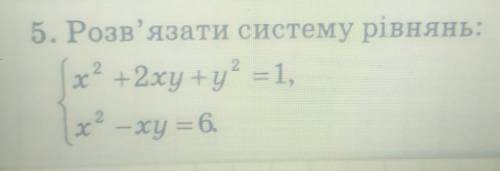
Другие вопросы по теме Алгебра
Популярные вопросы
- Втреугольника авс точка м середина стороны ас,угол вма=90°,угол авс=40°,угол...
2 - 2*sin^2pi/6-корень 3*cos pi/6-2*cos^2pi/3...
1 - Высота прямоугольного параллелепипеда ровна 7см а его основания имеет стороны...
1 - Высота горы ямантау на урале равна 1638 м. определите атмосферное давление...
1 - 2вариант. 1. вычислите: а). 477 · 85 - 7784 : 56; б). (147 · 29 — 22 800 :...
1 - Прочитайте текст, выполните к нему и ответьте на вопросы....
1 - Прочитайте. какую роль может играть ударение. спишите предложения, поставив...
2 - Рассчитать массу na, если в реакцию с ним вступило 20 г h2o...
3 - Определите кпд трансформатора, если в первичную обмотку подается мощность 2...
2 - Қазақ халқы бос уақытын қалай өткізген эссе...
2
Объяснение:
1)
x+y=-1. ⇒
2)
x+y=1. ⇒
ответ: (-2;1), (1,5;-2,5), (-1,5;2,5), (2;-1).