Решите задачу Коши для заданной автономной системы дифференциальных уравнений.
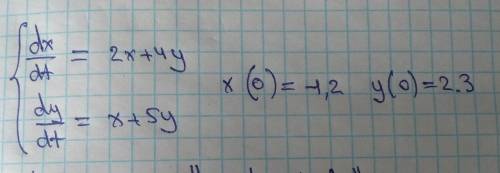
Другие вопросы по теме Алгебра
Популярные вопросы
- Сделайте уравнения, взявши числа которые я напишу за х (уровень...
3 - ответьте на вопрос: понравился ли вас рассказ а. п. чехова ,,...
2 - Ты помнишь сказки сергея козлова? прочитай короткую аннотации,поставленную...
3 - Как измерить силы трения скольжения и качения?...
3 - 2найдите значение выражения, составленного из дат. (указ петра...
3 - Жол ережелеріне қатысты құрамында сын есімі бар жұмбартар...
1 - 1)қасқыр мен ң іс - әрекетінде ұқсастық бар ма? венн диаграммасы...
1 - Составить предложения с союзами1)будто2)как будто3)то есть4)не...
2 - Найдите площади первого круга,радиус которого равен 12 дм,и площадь...
2 - С! много ! надо написать свойства 1) бензойной кислоты 2)олеиновой...
2
Продифференцируем первое уравнение:
Подставим в него соотношение для y' из второго уравнения:
Из полученного уравнения отнимем первое уравнение системы, умноженное на 5:
Составим характеристическое уравнение:
Найдем х':
Выразим у из первого уравнения:
Находим у:
Условие для задачи Коши:
От первого уравнения отнимем второе:
Выражаем из первого уравнения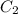 :
:
Частное решение: