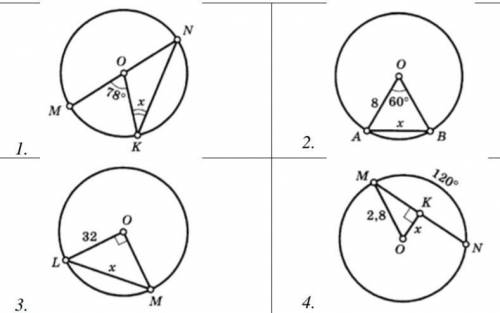
Решите задачи по готовым чертежам, в каждом из которых необходимо найти x​

ных и физиологических барьеров растения-хозяина, поэтому грибы

Для решения задачи, нам необходимо понять, как связаны между собой различные стороны и углы треугольников на чертеже. Давайте рассмотрим каждую задачу по отдельности и найдем значение x.

1. Задача №1:
Поскольку прямые AB и CD параллельны, у нас имеются параллельные прямые и трансверсаля. Это означает, что угол BAC и угол ADC являются соответственными углами и равны между собой. То же самое верно для угла ABC и угла ADC.
Таким образом, мы можем установить следующее равенство углов:
угол BAC = угол ADC
угол ABC = угол ADC
Затем мы видим, что угол BAC равен 87 градусов.
Итак, угол ADC также равен 87 градусам
Проанализируем второй треугольник. Угол ACD равен 87 градусам, и внешний угол треугольника ABC является суммой углов при вершине ACD.
Значит,
угол ABC = угол ACD + угол ADC
угол ABC = 87 + 87
угол ABC = 174 градуса

Таким образом, мы нашли значение угла ABC. Теперь, чтобы найти значение x, мы можем воспользоваться свойством, которое гласит, что сумма углов треугольника равна 180 градусов.
Значит, сумма углов треугольника ABC равна:
87 + 87 + x = 180
174 + x = 180
x = 180 - 174
x = 6

Ответ: x = 6

2. Задача №2:
В данной задаче мы также имеем параллельные прямые AB и CD, а значит углы, образованные этими прямыми, равны. Таким образом, угол BAC = угол ADC.
Из чертежа мы видим, что угол ADC равен 40 градусам.
Таким образом, угол BAC = 40 градусов.

Затем мы рассматриваем треугольник ABC. Угол ABC является внутренним углом треугольника ABC.
Значит, сумма углов треугольника ABC равна:
40 + 40 + x = 180
80 + x = 180
x = 180 - 80
x = 100

Ответ: x = 100

3. Задача №3:
В данном чертеже у нас имеется два параллельных участка AD и BC. Значит, углы, образованные этими участками, равны.
Угол BAC равен 120 градусам.
Значит, угол ABC равен 120 градусам.

Затем мы можем рассмотреть треугольник ABC. Известно, что сумма углов в треугольнике равна 180 градусов.
120 + 120 + x = 180
240 + x = 180
x = 180 - 240
x = -60

Ответ: x = -60

Таким образом, мы нашли значения x для каждой из задач.