Решите в действительных числах систему равнений ( не подбором) 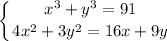
Другие вопросы по теме Алгебра
Популярные вопросы
- Підкресліть прийменникові сполучення у яких порушені правописні норми.відреагуйте...
3 - 1)укажите число нейтронов и электронов для 22ti. 2)укажите заряды частиц: 6c2e;...
2 - Склади по два речення iз дiэсловами теперiшнього часу iз дiэсловами майбутнього...
1 - Решите уравнение! зарание ! 10(0.1x++1)=15...
1 - Студент получил стипендию 600р. купюрами достоинством 50р. и 10.- всего 24 купюры....
1 - Какая масса соли образуется при взаимодействии 6 г ch3cooh с раствором naoh?...
3 - Мини сочинение что для тебя красота...
1 - Придумайте сложносочиненное предложение, осложненное причастным оборотом...
3 - Морфологический разбор слова торопливым...
1 - 1) найдите значение вы ражения 2√6*√2*8√3 2) 7.8*2.8/0.56 3)решите уравнения...
1
Вычтем из первого уравнения утроенное второе:
Второе уравнение превращается в
ответ: (4;3), (3;4)