Алгебра: Решите в целых числах уравнение x²-xy-2y²=7

Решите в целых числах уравнение
x²-xy-2y²=7

Ответы

thesketchyoup081qt 10.10.2020 17:13

$x^2-xy-2y^2=x^2-y^2-xy-y^2=(x-y)(x+y)-y(x+y)=\\=(x+y)(x-y-y)=(x+y)(x-2y)$

Мы разложили левую часть на два множителя. Число 7 — простое, поэтому оно может раскладываться ровно на две пары целых множителей: (1; 7) и (–1, –7). Тогда получим четыре системы:

Первая система:

$\begin{cases}x+y=1\\x-2y=7 \end{cases}\\\begin{cases} x=1-y\\1-y-2y=7\end{cases}\\-3y=6\\y=-2\\x=1-y=3$

Вторая система:

$\begin{cases}x+y=7\\x-2y=1\end{cases}\\\begin{cases}x=7-y\\7-y-2y=1\end{cases}\\-3y=-6\\y=2\\x=7-y=5$

Третья система:

$\begin{cases}x+y=-1\\x-2y=-7\end{cases}\\\begin{cases}x=-1-y\\-1-y-2y=-7\end{cases}\\1+y+2y=7\\3y=6\\y=2\\x=-1-y=-3$

Четвёртая система:

$\begin{cases}x+y=-7 \\ x-2y=-1\end{cases}\\\begin{cases}x=-7-y \\ -7-y-2y=-1\end{cases}\\7+y+2y=1\\3y=-6\\y=-2\\x=-7-y=-5$

ответ: (3; –2), (–3; 2), (5; 2), (–5; –2).

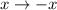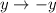P. S. Третью и четвёртую систему можно было бы не расписывать, если заметить, что при одновременной замене $x \rightarrow -x$ и $y \rightarrow -y$ значение выражения 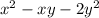x^2-xy-2y^2 не изменится. Это означает, что если (x; y) является решением, то (–x; –y) тоже является решением.

ПОКАЗАТЬ ОТВЕТЫ

stazagreen 07.01.2024 21:04

Для решения данного уравнения в целых числах, мы можем использовать метод подстановки или метод приведения уравнения к квадратному дискриминанту.

Метод подстановки:
Пусть мы предположим, что x и y являются целыми числами. Мы можем начать с подстановки целых чисел для x и y и поискать соответствующие значения, которые удовлетворяют уравнению.

Если мы попробуем значения x = 1 и y = 2, то получим:
(1)² - (1)(2) - 2(2)² = 1 - 2 - 8 = -9, что не равно 7.
Если мы попробуем значения x = 2 и y = 1, то получим:
(2)² - (2)(1) - 2(1)² = 4 - 2 - 2 = 0, что не равно 7.
Продолжим подставлять другие значения, пока не найдем такие, которые удовлетворяют уравнению.

Метод приведения к дискриминанту:
Мы можем привести уравнение к квадратному дискриминанту путем замены y^2 на t:
x² - xy - 2t = 7.

Затем, используя общую формулу для квадратных уравнений, мы можем решить это уравнение относительно x:
x = (y ± √(y² + 8t - 28))/2.

Теперь, чтобы найти целочисленные значения x и y, мы можем подставить различные значения для t и проверить, когда выражение под корнем имеет целочисленное значение.

Например, если мы попробуем t = 1, то получим:
x = (y ± √(y² + 8 - 28))/2,
x = (y ± √(y² - 20))/2.

Здесь, нам нужно найти такие значения y, при которых выражение под корнем (y² - 20) является квадратом целого числа.

Если мы попробуем y = 5, то получим:
x = (5 ± √(25 - 20))/2,
x = (5 ± √5)/2.

Это не даст нам целочисленные значения x и y. Мы можем продолжить подставлять различные значения для y и проверять, когда выражение под корнем становится квадратом целого числа.

Таким образом, решением данного уравнения x²-xy-2y²=7 в целых числах нет.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра