Решите уравнения:
1)x2/2-x=3x/2-x
2) y+4/y+2=2y-1/y
3) 5x-2/x+2=6x-21/x-3
Другие вопросы по теме Алгебра
Популярные вопросы
- Заполните пропуски: движение по окружности характеризуют угловой...
2 - Почему число неспареных электронов определяется путём формулы 8-номер...
3 - Текст рассуждение на тему почему герасим ушёл в деревню...
2 - Определите жанр произведения про кота ю.дмитриева....
1 - Составить предложения со словами : сыртқы бейне, ішкі дүние, киім...
3 - Вкаком случае можно писать в нонрп чат? 1.сообшить нонрп инфу 2.сообшить...
2 - Пассивный или активный залог? a lot of money was given to the animal...
3 - Сравните массы двух одинаковых по размерам капель бензина и спирта....
1 - Что такое синтетический заменитель кислоты ? ионы водорода входят...
3 - Представьте в виде произведения степень (-2) в 5 степени умножить...
3
Объяснение:
1)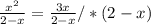
x² = 3x
x² - 3x = 0
x(x - 3) = 0
x₁ = 0
x₂ = 3
y(y + 4) - (y + 2)(2y - 1) = 0
y² + 4y - (2y² - y + 4y - 2) = 0
y² + 4y - 2y² + y - 4y + 2 = 0
y² + y + 2 = 0
D = b² - 4ac = 1 - 4*2 = -7
D < 0 корней нет
(x - 3)(5x - 2) - (x + 2)(6x - 21) = 0
5x² - 2x - 15x + 6 - (6x² - 21x + 12x - 42) = 0
5x² - 2x - 15x + 6 - 6x² + 21x - 12x + 42 = 0
-x² - 8x + 48 = 0
D = b² - 4ac = 64 - 4*(-1)*48 = 256
√D = 16
x₁ = (8 + 16)/(-2) = 24/(-2) = -12
x₂ = (8 - 16)/(-2) = (-8)/(-2) = 4