Решите уравнения :
1) sinx × cosx=sin35°
2) arcsin 2x = arccos x
Другие вопросы по теме Алгебра
Популярные вопросы
- 2. Укажіть речення, у якому є прикметник. 1. Один цвіт не робить вінка (Нар. тв.)....
2 - Open the hrackets using Present Perfect Possive 1.The light (to turn off) yet...
1 - А3. В какую сторону движется проводник с током, изображённый на рисунке?...
2 - Задание 1. Распределите имена существительные по графам в зависимости от разряда...
1 - В треугольнике САВ отметь угол, противолежащий стороне САВВСАСDА...
1 - придумайте текст про Ялту на английском 7 предложений (6 класс)...
2 - Запишите, что вы понимаете об Аладдине.Помагите ...
3 - А. Дополни диалоги, выбрав один из глаголов «rester» или «laisser». Qu est-ce...
3 - Дослідіть здатність хлоридної кислоти і натрій хлориду до взаємодії з аргентум(1)...
1 - Я не могу сделать это задание мне. ...
3
Объяснение:
1) 0,5·sin2x = sin35° ⇔ sin2x = 2·sin35° (1) ; так как y = sinx
возрастает в первой четверти , то sin35° > sin30° = 0,5 ⇒
2·sin35° > 1 ⇒ уравнение (1) не имеет решений
2) arcsin 2x = arccos x (2) , arccos x ≥ 0 для всех х ⇒ arcsin 2x ≥ 0
⇒ х ≥ 0 ; так как из области определения у = arcsin2x следует
, что х ≤ 0,5 , то уравнение (2) имеет решение только ,
если x ∈ [ 0 ; 0,5] , на этом отрезке левая часть уравнения
меняется от 0 до π/2 , а правая от π/3 до π/2 ⇒
уравнение ( 2) имеет решение , если множество
значений обеих частей не выходит за пределы [π/3 ; π/2] , но
на этом отрезке функция y = sinx - возрастает ⇒ уравнение ( 1 )
равносильно на [ 0 ; 0,5] следующему :
sin(arcsin2x) = sin(arccosx)
2x = ⇔ 4x² = 1 - x² ⇔ x² = 1/5 ⇒
⇔ 4x² = 1 - x² ⇔ x² = 1/5 ⇒
x =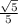 ( так как х ≥ 0)
( так как х ≥ 0)
функции , стоящие в левой и правой частях уравнения имеют
разную монотонность , поэтому сразу ясно , что уравнение
имеет не более одного корня , в этом случае его достаточно
" угадать " , но угадать не получилось , пришлось брать
синусы от обеих частей
f(x) = g(x) ⇔ h(f(x)) = h(g(x) ) , если h(x) - монотонна и значения
f и g входят в область определения функции h , поэтому
и пришлось доказывать , что значения f и g не выходят
за пределы первой четверти , а там синус возрастает и
поэтому законно брать синусы от обеих частей