РЕШИТЕ УРАВНЕНИЕ! (я сама решила, но мне нужно с кем-нибудь свериться)
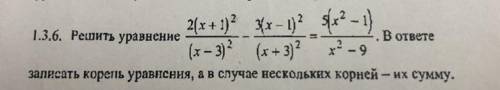
Другие вопросы по теме Алгебра
Популярные вопросы
- Выражение[tex] \sqrt{14 - 4 \sqrt{10} } + \sqrt{49 - 12 \sqrt{10}...
2 - Пшёоэ йоуёсётоба лойдб как расшифровать? с условием что каждая...
2 - Расставить правильно строчки, чтобы получился диалог...
3 - Утворіть із кожної пари речень одне, ускладнене дієприкметниковий...
1 - Соотнесите реки и их питание(все должны быть использованы) 25...
1 - Что показывает процентное отношение первого числа от второго...
2 - Проводники сопротмвлением 15 ом, 24 ом и 12 ом соединены последовательно....
1 - Нужно сообщение на тему войны в европе в век просвещения. надо...
1 - Лыжник весом 800h имеет опорную силу площадь обеих лыж 0,4м определите...
3 - Кто из майордов установил новую систему землеводиння...
3
Всё то же, но с другой заменой
Замена: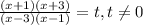
1)
2)
Сумма корней уравнения: