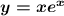Решите уравнение: y′-y/x=xe^x, y(1)=e
Другие вопросы по теме Алгебра
Популярные вопросы
- Через які точки проходить графік рівняння 5y-3x=-1...
2 - Футбол ойын ережесі бүзылғанда төрешінің әрекеті? А. Ысқырады В. Айкайлайды С....
3 - Мәтін бойынша сұрақтар: Дәрігер Дарханға қандай кеңес айтты? Не себепті ауруы...
1 - Фонетикалық талдау жасаңыз: журнал,құрастырушы,программа...
3 - Билет № 8 Үстеудің негізгі мағыналық түрлеріне мысал келтіріп айту. «Сапалы өнім»...
2 - 5.Kaкaя физическая величина определяется выражением (N/t) (N-число колебаний за...
1 - My cotte and croissants are not cold,aren t......
3 - Мідна кулька масою 89 г має порожнину. Кульку підвісили доДинамометра та занурили...
2 - Шаңғышыны мәреге қанша метр қалғанда бақылап қарайды? А.50 В. 80 С. 70 Д. 100...
1 - Live, in, which, is, sea, from, not, far, I, the, White, Severodvinsk.Составьте...
1
Умножим левую и правую часть уравнения на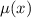 , которое вычисляется таким образом:
, которое вычисляется таким образом:
Имеем:
Заметим, что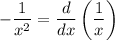 , получаем
, получаем
Воспользуемся тем, что левая часть уравнения - это дифференциал произведения двух функций.
Нашли общее решение линейного неоднородного уравнения.
Найдем теперь частное решение, подставляя начальные условия.
Получим частное решение задачи Коши: