Решите уравнение :
x³·√x - 3x·√x + x + 1 = 0
Другие вопросы по теме Алгебра
Популярные вопросы
- В чистой воде растворено некоторое количество спирта. Масса раствора...
2 - іть з завданням в профеле ів за то завд...
1 - Сделать нужно только все задания с нумеровкой А и одно задание...
3 - ... история. сообщение по культуре в 18 веке в европе...
1 - Партия принявшие идеи неоконсерватизма обещали сочетать ... ?...
2 - Сочинение на тему рассуждение почему я считаю этого человека своим...
2 - Две стороны треугольника равны 6,8 и 3,6см высота проведена к...
2 - Всем ку, нужно написать текст 10-15 предложений употребив все...
2 - Кто в бравл играет скинти яди и сколька кубков...
1 - дан равнобедренный треугольник ABC у которого AB = BC =14 см,...
1
(см. объяснение)
Объяснение:
Так как работаем с неотрицательными числами, то:
Из исходного уравнения следует, что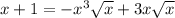 .
.
Тогда получим:
Решим это неравенство:
Подставим оба значения в исходное уравнение и убедимся, что подходит только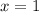 , а значит он является корнем.
, а значит он является корнем.
Уравнение решено!