Алгебра: Решите уравнение: (x^2 + 4x + 8)^2 + 3x^3 + 14x^2 + 24x = 0

группируем Данное уравнение является возвратным уравнением четвёртой степени, поскольку . Так как х=0 не является решением / Произведём замену переменных: Пусть В результате замены переменных получаем вс уравнение. Cчитаем дискриминант: Дискриминант положительный Уравнение имеет два различных корня: Теперь решение исходного уравнения разбивается на отдельные случаи. Случай 1 /· умножаем на х для того, чтобы избавиться от знаменателя Cчитаем дискриминант:...

Решите уравнение: (x^2 + 4x + 8)^2 + 3x^3 + 14x^2 + 24x = 0

Ответы

wavystrong 23.05.2020 21:21

(x^2+4x +8)^2 +3x^3 +14x^2+24x=0

x^4+16x^2+64+8x^3+16x^2+64x+3x^3+14x^2+24x=0

x^4+11x^3+46x^2+88x+64=0

Это возвратное уравнение четвёртой степени, так как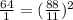 $\frac{64}{1}=(\frac{88}{11})^2$ . Поскольку х=0 не является решением, разделив левую часть на 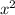x^2 , получим

$x^2+11x+46+\frac{88}{x}+\frac{64}{x^2}=0$

$x^2+\frac{8^2}{x^2}+16+11x+\frac{88}{x}+30=0$

$(x+\frac{8}{x})^2+11(x+\frac{8}{x})+30=0$

Произведём замену: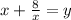 $x+\frac{8}{x}=y$

y^2+11y+30=0

по теореме Виета: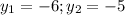 y_1=-6; y_2=-5

Делаем обратную подстановку:

$x+\frac{8}{x}=-6$

x^2+6x+8=0

по теореме Виета: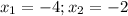 x_1=-4; x_2=-2

$x+\frac{8}{x}=-5$

x^2+5x+8=0

не имеет корней, так как дискриминант отрицательный: D=5^2-4*8=-7<0

ответ: -4; -2.

ПОКАЗАТЬ ОТВЕТЫ

ahmedova3 23.05.2020 21:21

$(x^{2}+4x+8)^{2}+3x^{3}+14x^{2}+24x=0$

$x^{4}+16x^{2}+64+8x^{3}+16x^{2}+64x+3x^{3}+14x^{2}+24x=0$

группируем

$x^{4}+(8x^{3}+3x^{3})+(16x^{2}+16x^{2}+14x^{2})+(64x+24x)+64=0$

$x^{4}+11x^{3}+46x^{2}+88x+64=0$

Данное уравнение является возвратным уравнением четвёртой степени, поскольку

$\frac{64}{1}=(\frac{88}{11})^{2}$ . Так как х=0 не является решением

$x^{4}+11x^{3}+46x^{2}+88x+64=0$ / $x^{2}$

$x^{2}+11x+46+\frac{88}{x}+\frac{64}{x^{2}}=0$

$x^{2}+\frac{64}{x^{2}}+11x+\frac{88}{x}+46=0$

$x^{2}+\frac{8^{2}}{x^{2}}+16+11x+\frac{88}{x}+30=0$

$(x^{2}+\frac{8^{2}}{x^{2}}+16)+(11x+\frac{88}{x}+30)=0$

$(x+\frac{8}{x})^{2}+11(x+\frac{8}{x})+30=0$

Произведём замену переменных:

Пусть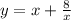 $y=x+\frac{8}{x}$

В результате замены переменных получаем вс уравнение.

$y^{2}+11y+30=0$

Cчитаем дискриминант:

$D=11^{2}-4\cdot1\cdot30=121-120=1$

Дискриминант положительный

$\sqrt{D}=1$

Уравнение имеет два различных корня:

$y_{1}=\frac{-11+1}{2\cdot1}=\frac{-10}{2}=-5$

$y_{2}=\frac{-11-1}{2\cdot1}=\frac{-12}{2}=-6$

Теперь решение исходного уравнения разбивается на отдельные случаи.

Случай 1

$x+\frac{8}{x}=-5$ /·

умножаем на х для того, чтобы избавиться от знаменателя

$x^{2}+8=-5x$

$x^{2}+5x+8=0$

Cчитаем дискриминант:

$D=5^{2}-4\cdot1\cdot8=25-32=-7$

Дискриминант отрицательный, следовательно уравнение не имеет действительных решений.

Случай 2

$x+\frac{8}{x}=-6$ /·

умножаем на х для того, чтобы избавиться от знаменателя

$x^{2}+8=-6x$

$x^{2}+6x+8=0$

Cчитаем дискриминант:

$D=6^{2}-4\cdot1\cdot8=36-32=4$

Дискриминант положительный

$\sqrt{D}=2$

Уравнение имеет два различных корня:

$x_{1}=\frac{-6+2}{2\cdot1}=\frac{-4}{2}=-2$

$x_{2}=\frac{-6-2}{2\cdot1}=\frac{-8}{2}=-4$

ответ: $x_{1}=-2$ ; $x_{2}=-4$

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

DoKim01 08.06.2019 23:20

Арифметическая прогрессия задана формулой an= -5,5+4,1* n .найти a12. !...

lavika1 08.06.2019 23:20

Выписаны первые несколько членов арифметической прогрессии: 6; 10; 14; найдите ее одиннадцатый член....

Rawree258 08.06.2019 23:20

Вящике имеется 15 деталей, из которых 10 стандартные.сборщик берёт наугад три детали. найти вероятность того, что две из взятых деталей стандартные....

nukita200230 08.06.2019 23:20

1.какое наименьшее значение и при каком значении переменной выражение x^2+16х-40 ? p.s x^2 это x во 2 степени 2.сколько килограммов 20-процентного и сколько килограммов...

shakirqasanov 08.06.2019 23:20

Сумма трех чисел, составляющих убывающую арифметическую прогрессию,равна 60. если от первого числа отнять 10, от второго отнять 8, а третье число оставить без изменения,...

sabina9262 08.06.2019 23:20

Сократить и решить выражение со значениями ?...

miakakashka 08.06.2019 23:20

Найдите значения выражения при значении a = 2,5...

Лиза45111 08.06.2019 23:20

Решить надо, ) 1) (x-3y)^2-4m^2 2) делится ли число 99^3-53^3 на 47? ответ поясните)...

shaxrizat1 08.06.2019 23:20

Катет прямоугольного треугольника равен 6 корней из 11 и 2. найдите синус наименьшего угла....

olhkasianchuk 08.06.2019 23:20

1)игральную кость бросают дважды. найдите вероятность того, что наибольшее из двух выпавших чисел равно 5. 2)игральную кость бросают дважды. найдите вероятность того,...

Решите уравнение: (x^2 + 4x + 8)^2 + 3x^3 + 14x^2 + 24x = 0

Популярные вопросы