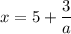Решите уравнение 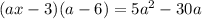 в зависимости от значений параметра
в зависимости от значений параметра 
Другие вопросы по теме Алгебра
Популярные вопросы
- Обчисліть масу пропіонової кислоти, яка утвориться при окисненні пропанолу...
2 - Что мы видим на этих картинках?какой общей темой можно объяденить данные...
2 - Составьте 7-8 уравнений реакций получения синтетических органических полимеров...
3 - Решите очень нужна норм оценка Р в матике не сильно разбираюсь...
1 - Очень очень через 20 минут сдавать!...
1 - решить задачи из лабораторной работы...
3 - 1 задание: решите тест. 1.Сердце у птиц: А. четырехкамерное; Б. трехкамерное...
3 - Построить и описать график функции: 1) у=(х+2)^4+12) у=4sinx -3 3) у=tg(x−п/6)...
2 - Основание прямой призмы-прямоугольный треугольник с площадью 4дм^2 и углом...
3 - Абай Құнанбаев кім? Жазайлары: Жазда ауа райы қандай болады? Жазда балалар...
2
1) Если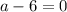 , то есть
, то есть 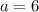 , то имеем уравнение
, то имеем уравнение 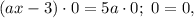 решением которого является любое число.
решением которого является любое число.
2) Если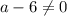 , то есть
, то есть 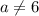 , то
, то 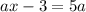
Перепишем уравнение в виде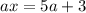
2.1) Если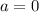 , то имеем уравнение
, то имеем уравнение 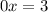 , которое не имеет решений.
, которое не имеет решений.
2.2) Если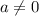 , то
, то 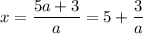
ответ: если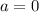 , то нет корней; если
, то нет корней; если 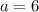 , то
, то  — любое число; если
— любое число; если 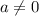 и
и 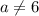 , то
, то