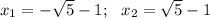Решите уравнение
в) (x + 1)^4 − 4(x + 1)^2 − 5 = 0
Другие вопросы по теме Алгебра
Популярные вопросы
- Сходства и различия по критериям для сравнения лютера и кальвина...
3 - 1/3x(0,152: 0,5-0,4: 100) как это решить?...
3 - 1)медь имеет изотопы с массовыми числами 65и63. укажите для каждого изотопа...
1 - Как обозначить на контурной карте моря, заливы и проливы...
2 - Кпримеру 50, 50 если разложить на простые числа получается 2×5×5 на как...
1 - Опера иван сусанин напойте мелодию рондо антониды и сравните её с мелодией...
2 - Выбрать запись ,показывающие что число m в 9 раз больше числа n 1)m: 9=n2)m*9=n...
3 - 70 ! 1) sinx=a^2-1 2)0.5-sin(11p/12)...
1 - Что такое натуральные числа? это от 1 до 9?...
1 - Вкорзине лежало 47 грибов, 12 грибов , 26 грибов засолили, а остальные...
3
Решаем методом замены переменной.
Пусть (х+1)²=t, тогда:
Решаем данное квадратное уравнение теоремой Виета. Получим корни t1=5 и t2=-1.
Вернём замену.
(х+1)²=t, то есть (х+1)²=5 или (х+1)²=-1
Второй корень отметаем, так как что-то в квадрате не может дать -1. Решаем первое уравнение:
Это и есть ответ.
Сделаем замену
Подставляем значения
ответ: