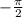Решите уравнение. В ответе запишите наибольший отрицательный корень уравнения (в градусах) умноженный на 13. 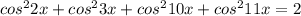
Другие вопросы по теме Алгебра
Популярные вопросы
- Тарифные преференции в отношении развивающихся стран предоставляются при выполнении...
2 - Предоставление тарифных преференций развивающимся странам сопряжено с рядом ограничений,...
1 - От уплаты акцизов освобождается спиртосодержащая парфюмерно-косметическая продукция,...
3 - В таможенной статистике внешней торговли количественный учет товаров ведется по...
3 - Правило кумулятивности означает, что товар закупается у фирмы, зарегистрированной...
1 - Нетарифные меры имеют опосредующее значение, служа _ механизмом в регулировании...
3 - Ввоз товаров в качестве_ в уставный (складочный) капитал может быть осуществлен...
3 - Продукция морского промысла, добытая и произведенная в Мировом океане судами данной...
2 - В разделе VI Товарной номенклатуры внешнеэкономической деятельности сгруппирована...
1 - Таможенное оформление товаров, не входящих в закрытый перечень, осуществляется в...
3
Наибольший отрицательный корень будет при n= -1 :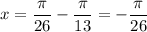 ,
, 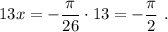
Ниже↓
Объяснение:
cos²α=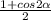 / Применим эту формулу для левой части и 1\2 сразу вынесем за скобки
/ Применим эту формулу для левой части и 1\2 сразу вынесем за скобки
1\2*(1+cos4х+1+cos6х+1+cos20х+1+cos22х)=2 |:2
1+cos4х+1+cos6х+1+cos20х+1+cos22=4
cos4х+cos6х+cos20х+cos22=0 Применим сумму косинусов:
2 cos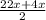 cos
cos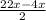 +2cos
+2cos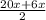 cos
cos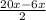 =0
=0
2cos13x*cos9x+2cos13x*cos7x=0
2cos13x*(cos9x+cos7x)=0 |:2
cos13x*(2cos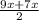 *cos
*cos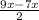 =0
=0
2*cos13x*cos8x*cosx=0
cos13x=0 , 13х=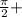 πn ,х=
πn ,х=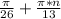 , n∈Z.
, n∈Z.
cos8x=0 , 8х=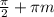 ,х=
,х=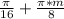 , m∈Z.
, m∈Z.
cosx=0 , x=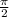 +πk , k∈Z
+πk , k∈Z
Наибольший отрицательный корень , по смыслу , ближе всех к нулю. Это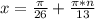 /При n=-1 :
/При n=-1 : 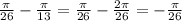 . Если умножить на 13 , то будет
. Если умножить на 13 , то будет