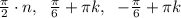Решите уравнение
Другие вопросы по теме Алгебра
Популярные вопросы
- Школа предоставила отчёт: всего в школе 60 шестиклассников, из них...
1 - Из посёлка одновременно в одном направлении выехали два всадника....
2 - Как перевести текст почему why hares have got long ears часть 4...
3 - Впервый день в магазин завезли 40% всего картофеля, а во второй...
1 - При каких значениях а верно равенство -|-а|=-а...
2 - Красное разобрать (морфологический)...
3 - За день вид двох корив надоилы по 18л молока и ще вид трех-по 17л.скилькы...
2 - Write like/likes. 1 i like cats. 2 you chicken. 3 he chips....
2 - Скажите значения слов меценат,фартуна и вулкан.(как можно длиннее)...
2 - Анализ стихотворения «шаганэ ты моя, шаганэ» с. есенина...
1
Произведение равно 0, когда один из множителей равен 0
ответ: