1. Алгебра
  2. Решите уравнение: [tex]sin(x)+sin(3x)+sin(5x)+sin(7x)=0[/tex]

Решите уравнение: sin(x)+sin(3x)+sin(5x)+sin(7x)=0

newagain newagain    2   04.01.2020 08:53    65

Ответы
aurantiuma aurantiuma  10.10.2020 23:51

\sin x+\sin3x+\sin5x+\sin7x=0

Сгруппируем слагаемые следующим образом:

(\sin x+\sin7x)+(\sin3x+\sin5x)=0

Воспользуемся формулой для суммы синусов:

2\sin\dfrac{x+7x}{2}\cos\dfrac{x-7x}{2}+2\sin\dfrac{3x+5x}{2}\cos\dfrac{3x-5x}{2}=0

2\sin4x\cos(-3x)+2\sin4x\cos(-x)=0

Воспользуемся четностью функции косинуса:

2\sin4x\cos3x+2\sin4x\cos x=0

Вынесем общий множитель за скобки:

2\sin4x(\cos3x+\cos x)=0

Для суммы косинусов воспользуемся соответствующей формулой:

2\sin4x\cdot2\cos\dfrac{3x+x}{2}\cos\dfrac{3x-x}{2}=0

2\sin4x\cdot2\cos2x\cos x=0

4\sin4x\cos2x\cos x=0

Уравнение распадается на совокупность трех уравнений:

\left[\begin{array}{l} \sin4x=0 \\ \cos2x=0 \\ \cos x=0 \end{array}

\left[\begin{array}{l} 4x=\pi n \\ 2x=\frac{\pi}{2}+\pi n \\ x=\frac{\pi}{2}+\pi n \end{array}

\left[\begin{array}{l} x=\frac{\pi n}{4} \\ x=\frac{\pi}{4}+\frac{\pi n}{2} \\ x=\frac{\pi}{2}+\pi n \end{array}

Заметим, что корни, даваемые второй и третьей серией, также даются и первой серией. Значит, более простая запись решения следующая:

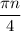x=\dfrac{\pi n}{4}, \ n\in Z

ответ: \dfrac{\pi n}{4}, где n - целые числа

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Arina4dyuzhova Arina4dyuzhova  20.11.2021 20:43
Со пару линейных функций с избражением графиков. 7 класс алгебра >...
Dasha1648938190 Dasha1648938190  20.11.2021 20:41
Решите задания на картинке 7 класс....
TaKuRGRAF TaKuRGRAF  20.11.2021 20:41
Возведи одночлен 2a5m3 в Квадрат....
nysha046 nysha046  20.11.2021 20:40
Y=6x−7 узнать точку пересечения...
Лисёнка2005 Лисёнка2005  20.11.2021 20:39
Постройте графики функций а)у=6х-4 б)у=-2х+7 в)у=7х г)у=-2х оччень нужн...
гот12 гот12  20.11.2021 20:37
Определи значение x, соответствующее значению y=0 для линейного уравнения 12x+14y=60....
SUPERMARY007 SUPERMARY007  20.11.2021 20:35
Айди значение y, соответствующее значению x=0 для линейного уравнения 4x+4y−20=0. быстрее...
nadijagordijenp07vwr nadijagordijenp07vwr  20.11.2021 20:34
При каких значениях аргумента : 1) Значение функции f (x) = 5/x + 4 будет равно 32) Значение функции g (x) = 5 x + 1 / 3. + 4 будет равно 11...
Maria2009 Maria2009  01.03.2020 16:23
Желательно с решением. Заранее...
valiafurch valiafurch  01.03.2020 16:23
Очень Найдите значение производной функции у = log7 (cos2х) при x=пи/8А.-(2/ln7)B.2/ln7C.-(2*sqrt(2)/ln7)D.2*ln7​...

Популярные вопросы