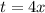Решите уравнение: 
Другие вопросы по теме Алгебра
Популярные вопросы
- Как сделать английский язык 4 класс...
3 - 1. Объясните выделенные слова. Составьте с ними предложения. Входить –...
3 - Напиши небольшой текст из 5-7 предложений на тему : Как надо учиться?...
1 - с географией!! «Современные формы рельефа» Какое бывает выветривание? Почему...
1 - Точки Ао, Во, со лежать на одній прямій і проектуютьсяна площину а в точках...
3 - Установи соответствие между термином и определением....
1 - Информация о происхождении игры бестас...
1 - Арман Сколько равных частей нужно разделить на единицы, чтобы обозначить...
2 - Дієслова недоконаного виду є виділене в тексті слово 1.Уявити 2.Життя 3.Передали...
3 - ответь как можно скорее на вопросы по биологии...
1
Получаем: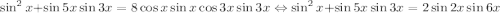 ; Подберем такие a и b, что
; Подберем такие a и b, что 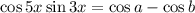 ; Это легко сделать по формуле суммы косинусов. Получаем систему
; Это легко сделать по формуле суммы косинусов. Получаем систему 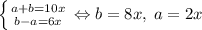 ; Аналогично делаем и в правой части уравнения. В итоге (после умножения на 2 обеих частей):
; Аналогично делаем и в правой части уравнения. В итоге (после умножения на 2 обеих частей):
Наконец,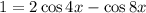 ; Сделаем замену:
; Сделаем замену: