РЕШИТЕ УРАВНЕНИЕ! ТЕМА: ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ
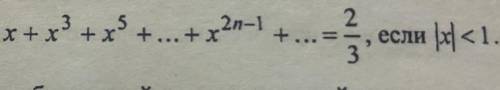
Другие вопросы по теме Алгебра
Популярные вопросы
- Установите соответствие между видами малых социальных групп и...
2 - Свидетельство о праве на наследство выдается нотариусом по месту...
3 - Приятие целей и средств данной социальной общнсти даже путем...
3 - Верны ли определения?А) приобретая права на определенную (известную)...
2 - Верны ли определения?А) Юридическое лицо вправе выступать в качестве...
2 - Верны ли определения?А) Принятие наследства через представителя...
2 - Завещание является односторонней сделкой, которая создает права...
3 - Верны ли определения?А) Общий срок принятия наследства - срок...
3 - Наследник, умерший после открытия наследства, но не успевший...
3 - Нотариус не позднее чем через _ дней со дня представления свидетельства...
1
0,5
Объяснение:
Слагаемые левой части представляют собой бесконечную геометрическую прогрессию с первым членом x и знаменателем x². Так как |x| < 1, x² < 1. Значит, это бесконечно убывающая геометрическая прогрессия, левую часть можно расписать по формуле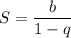 :
:
Из полученных корней подходит только x = 0,5.