Решите уравнение sin^6 x+cos^6 x=a(sin^4 x+cos^4 x) при всех действительных значениях параметра a.
Другие вопросы по теме Алгебра
Популярные вопросы
- «напишите небольшое сочинение по картине а иванова подвиг молодова киевлянина...
2 - Как приготовить раствор 250 г 15% хлорида калия, должен получить, сколько воды?...
2 - Составте 2 предложение со слово мәктәп и 2 предложения со словам укытучы надо...
1 - Решить уравнения 1)6х-х+18=43; 2)9у+8у=136; 3)992÷(130-к)=8; 4)(148-а)×31=1581...
2 - Найти из стехотворения дары терака метафоры, эпититы, сравнения...
2 - Придумайте 5 похожих тем (дружба и вражда)...
3 - Написать 4 примера к слову тропа,как эпитет,метафора,сравнение,олицетворениее...
3 - Где находятся исток реки печора? в каком напровлении текут её воды?...
2 - Составьте и запишите текст на тему карабах...
1 - Оприделите какие общественно- политические, нравственные вопросы затрагивает...
3
Уравнение имеет решение, если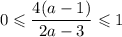 откуда получаем
откуда получаем 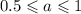
Для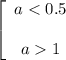 уравнение решений не имеет.
уравнение решений не имеет.