Решите уравнение
Sin^3x+sinx+√2= √2cos2x
Отберите корни уравнений на отрезке [3п/2;3п]
Другие вопросы по теме Алгебра
Популярные вопросы
- Вычисли объём водорода, который выделится в результате взаимодействия 9,75...
3 - Сумма корней уравнения 7х(2)+14х=0 равна: 1) 22) -23) 74) -7...
1 - 4факта о внешней и внутренней политике ханства хакназара.можно побыстрее...
1 - Напишите короткое сочинение что я больше всего люблю про велосипед. с чувствами...
2 - Предложения: уже совсем вечерело, мне не спится из за ветра, его сильно...
2 - Почему в первом случае вакол не является предлогом? а во втором является?...
3 - Написати твір « щоб я додав до конституції сша»...
3 - Какие факторы оказывают положительное влияние на состояние вашего здоровья...
1 - Написать пересказ по“ сказка о потерянном времени„ евгений львович шварц.в...
1 - Твір на тему тарас шевченко великий син україни...
3
Решим квадратное уравнение относительно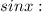
x ∈ ∅