Решите уравнение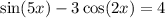
с точны объяснением и с рисунком​

Объяснение:

Функции sin и cos определены от -1 до 1. Равенство sin 5x - 3cos 2x = 4 возможно только в одном случае:

{sin 5x = 1

{cos 2x = -1

{5x = Pi/2 + 2Pi*m

{2x = Pi + 2Pi*k

{x = Pi/10 +2/5*Pi*m

{x = Pi/2 + Pi*k

При m = 1 получаем:

x = Pi/10 + 2Pi/5 = Pi/10 + 4Pi/10 = 5Pi/10 = Pi/2

При каком m получим x = Pi/2 + Pi = 3Pi/2 (k = 1)?

3Pi/2 - Pi/10 = 15Pi/10 - Pi/10 = 14Pi/10 = 7Pi/5 = 2Pi/5*m

m = 7/2 = 3,5 - не целое.

При каком m получим x = Pi/2 + 2Pi = 5Pi/2 (k = 2)?

5Pi/2 - Pi/10 = 25Pi/10 - Pi/10 = 24Pi/10 = 12Pi/5 = 2Pi/5*m

m = 6 - целое.

ответ: x = Pi/2 + 2Pi*n, n прин. Z