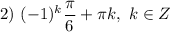Решите уравнение С решением
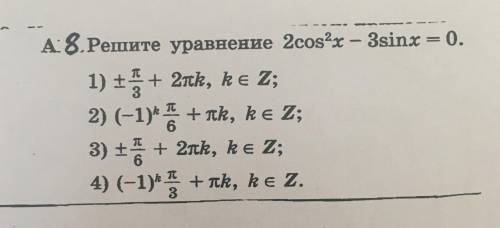
Другие вопросы по теме Алгебра
Популярные вопросы
- Что образуется в результате фотосинтеза?...
3 - Какие карты нужно использовать при описании реки...
2 - Проблемы и пути модернизации российского образования...
2 - Переведите в метры 5м 7дм= 3м 4см=...
3 - 1. укажите, какие из ниже утверждений не соответствуют действительности: а)...
3 - Найдите наименьшее и наибольшее значения функции: а) y = x^2 + 4x - 3...
2 - Какие факторы активизации национально освободительного движения в азии и африки...
3 - Решение обязательно! при каких r окружность с центром (-3; 4) и радиусом r не...
2 - Краткий рассказ о великом новгороде и переяславле -залесском...
1 - Люди ! ! сама дуб дубом в этом( хотя бы пару слов образуйте и запишите формы...
2
Замена: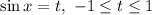
Обратная замена:
ответ: