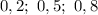Решите уравнение, с полным и понятным решением. $(5x+2)\cdot \sqrt{1-x}+(5x-7)\cdot \sqrt{x}=0$

Ответы

sunnybunnyka 14.07.2020 19:18

(5x + 2)√(1 - x) + (5x - 7)√x = 0

ОДЗ подкоренные выражения неотрицательны

1 - x ≥ 0 x ≤ 1

x ≥ 0

x ∈ [0 1]

(5x + 2)√(1 - x) = (7 - 5x )√x

при таком ОДЗ 7-5х > 0 (5x+2) > 0 корни тоже больше равны 0

смело возводим в квадрат

(5x + 2)²√(1 - x)² = (7 - 5x )²√x²

(25x² + 20x + 4)(1 - x) = (49 - 70x + 25x²)x

25x² + 20x + 4 - 25x³ - 20x² - 4x = 49x - 70x² + 25x³

50x³ - 75x² + 33x - 4 = 0

50x³ - 25x² - 50x² + 25x + 8x - 4 = 0

25x²(2x - 1) - 25x(2x - 1) + 4(2x - 1) = 0

(2x - 1)(25x² - 25x + 4) = 0

Dвторой скобки = 25² - 4*4*25 = 625 - 400 = 225 = 15²

x12 = (25 +- 15)/50 = 1/5 4/5

(2x - 1)(x - 1/5)(x - 4/5) = 0

(2x - 1)(5x - 1)(5x - 4) = 0

x1 = 1/2

x2 = 1/5

x3 = 4/5

все корни входят в ОДЗ [0 1]

ПОКАЗАТЬ ОТВЕТЫ

SherriBlendi 14.07.2020 19:18

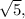Займусь своим любимым делом - упрощением уравнения. Но сначала выпишем ОДЗ: $x\in[0;1] -$ это очевидное следствие наличия двух радикалов. Далее: обращаю внимание на то, что в двух случаях "x" входит в уравнение с коэффициентом 5. А ведь скорее всего придется в квадрат возводить... В общем, домножаю уравнение на $\sqrt{5},$ занося сразу этот множитель под знаки радикалов:

$(5x+2)\cdot\sqrt{5-5x}+(5x-7)\cdot\sqrt{5x}=0; 5x=t\in[0;5];$

$(t+2)\cdot\sqrt{5-t}+(t-7)\cdot \sqrt{t}=0.$

На мой взгляд, уравнение стало выглядеть чуть привлекательней. Но это не предел. В уравнение неизвестная входит четыре раза. Надо бы уменьшить. Проверяем подстановкой, является ли решением t=0 - не является. Поэтому можно поделить уравнение на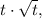 $t\cdot \sqrt{t},$ записав теперь его в виде

$(1+\frac{2}{t})\cdot\sqrt{\frac{5}{t}-1}+(1-\frac{7}{t})=0; \frac{1}{t}=p\in[\frac{1}{5};+\infty);$

$(1+2p)\cdot\sqrt{5p-1}=7p-1; p\ge\frac{1}{5}\Rightarrow p\ge\frac{1}{7},$

то есть это уравнение можно смело возводить в квадрат без боязни приобрести лишние корни:

(1+4p+4p^2)(5p-1)=49p^2-14p+1; 20p^3-33p^2+15p-2=0;

угадываем p=1; делим столбиком или угадываем разложение любым другим доступным ниже нашего достоинства говорить о таких мелочах, когда решаешь такую продвинутую задачу):

(p-1)(20p^2-13p+2)=0.

Итак, одно решение у нас уже есть (надо только не забыть в конце вернуться к первоначальной переменной), остается решить квадратное уравнение. Желающие могут вычислять дискриминант, мы же продолжим идти путем упрощенчества. Домножим уравнение

20p^2-13p+2=0 на 20 и сделаем замену (последнюю!) 20p=q:

$q^2-13q+40=0; (q-8)(q-5)=0; \left [ {{q=8} \atop {q=5}} \right. ; \left [ {{p=2/5} \atop {p=1/4}} \right. ; \left [ {{t=5/2} \atop {t=4}} \right. ; \left [ {{x=1/2} \atop {x=4/5}} \right.$