1. Алгебра
  2. Решите уравнение (полное

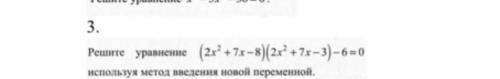
Решите уравнение (полное решение


Решите уравнение (полное решение

Бата194 Бата194    1   22.11.2020 11:15    5

Ответы
Dabby1 Dabby1  22.12.2020 11:17

(2x² + 7x - 8)(2x² + 7x - 3) - 6 =0

Сделаем замену :

2x² + 7x - 8 = m     ⇒   2x² +7x - 3 = m + 5

m * (m + 5) - 6 = 0

m² + 5m - 6 = 0

По теореме Виета :

m₁ = - 6     m₂ = 1

1) 2x² + 7x - 8 = - 6

2x² + 7x - 2 = 0

D = 7² - 4 * 2 * (- 2) = 49 + 16 = 65

x_{1}=\frac{-7-\sqrt{65} }{4}\\\\x_{2}=\frac{-7+\sqrt{65}}{4}

2) 2x² + 7x - 8 = 1

2x² +7x - 9 = 0

D = 7² - 4 * 2 * (-9) = 49 + 72 = 121 = 11²

x_{3}=\frac{-7-11}{4}=\frac{-18}{4}=-4,5\\\\x_{4}=\frac{-7+11}{4}=1

ПОКАЗАТЬ ОТВЕТЫ
thienla0 thienla0  22.12.2020 11:17

-4,5; \quad \frac{-7-\sqrt{65}}{4}; \quad \frac{-7+\sqrt{65}}{4}; \quad 1;

Объяснение:

(2x^{2}+7x-8)(2x^{2}+7x-3)-6=0;

Введём замену:

t=2x^{2}+7x.

Перепишем исходное уравнение с учётом замены:

(t-8)(t-3)-6=0;

t^{2}-3t-8t+24-6=0;

t^{2}-11t+18=0;

Решим уравнение при теоремы Виета:

\left \{ {{t_{1}+t_{2}=11} \atop {t_{1} \cdot t_{2}=18}} \right. \Leftrightarrow \left \{ {{t_{1}=2} \atop {t_{2}=9}} \right. ;

Вернёмся к замене:

2x^{2}+7x=2;

2x^{2}+7x-2=0;

D=b^{2}-4ac;

D=7^{2}-4 \cdot 2 \cdot (-2)=49+16=65;

x_{1}=\frac{-b+\sqrt{D}}{2a};

x_{1}=\frac{-7+\sqrt{65}}{2 \cdot 2}=\frac{-7+\sqrt{65}}{4};

x_{2}=\frac{-b-\sqrt{D}}{2a};

x_{2}=\frac{-7-\sqrt{65}}{4};

2x^{2}+7x=9;

2x^{2}+7x-9=0;

D=b^{2}-4ac;

D=7^{2}-4 \cdot 2 \cdot (-9)=49+72=121;

x_{1}=\frac{-b+\sqrt{D}}{2a};

x_{1}=\frac{-7+\sqrt{121}}{2 \cdot 2}=\frac{-7+11}{4}=\frac{4}{4}=1;

x_{2}=\frac{-b-\sqrt{D}}{2a};

x_{2}=\frac{-7-\sqrt{121}}{2 \cdot 2}=\frac{-7-11}{4}=\frac{-18}{4}=-4,5;

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
дагаыоукм дагаыоукм  03.04.2020 14:13
Самостоятельная работа Алгебра 8 класс​...
daniilf02mail daniilf02mail  03.04.2020 14:14
ОЧЕНЬ дата рождения если что 06.09 ( )...
TOPTopTOP1vvv TOPTopTOP1vvv  03.04.2020 14:14
Диагонали AC и BD прямоугольника ABCD пересекаются в точке О, ВО=24,АВ-45.Найдите АС...
mkashkan mkashkan  03.04.2020 14:18
1)Вычислить угловой коэффициент касательной к параболе y=x^2+x-1 в точках (1;1) и (2;5) 2) найти производное функции y=3 в вверху корня √xcosx y= sinx / cosx+1...
ra1si1ka1 ra1si1ka1  03.04.2020 14:06
Довести, що сума двох взаємно обернених додатних дробів завжди більша двох...
ArtMaster455 ArtMaster455  03.04.2020 14:08
Промежуток (-п/2; 5п/2), где находится?...
protivnuy protivnuy  30.12.2020 10:29
Решение уравнений. Урок 8 Уравнение (х - 1Хх – 2Xх - 3Xх – 4) +1 = 0 приведи к квадратному.Найдите решение данного уравнения​...
lutaasasa5p08d7e lutaasasa5p08d7e  30.12.2020 10:26
Параграф 1 числовые последовательности вместо вопросительного знака поставьте нужное число без обмана​...
bilpi bilpi  30.12.2020 10:24
5. Найдите: область определения функции y=2х-9​...
Otlichnica999 Otlichnica999  30.12.2020 10:23
Уравнение (х2 - 4х – 1) (х2 - 4х + 5) + 9 = 0 приведи к квадратному.Найди решение данного уравнения.​...

Популярные вопросы