Решите уравнение (подробно, с объяснениями)
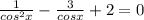
Другие вопросы по теме Алгебра
Популярные вопросы
- Определите падение реки, если h истока 4000 м, h устья 50 м (h-высота)...
2 - Решите уравнение d+ 2девятых=1--1 девятая...
1 - Вы собираетесь в поход какой рюкзак соберетесь с узким или широким...
3 - Кто и вкакой периуд времени утвердил первый свод законов на руси...
1 - Однокоренные слова к слову застеклена...
3 - Что такое морфологический разбор? и как его найти...
2 - Установите ,каким образом в 1-2 классов понятия: а)деление; б)нечетное...
2 - Масса (г) 15% раствора хлорида калия, в которой следует растворить...
1 - Решите с уравнения : из 830 г шерсти связали 4 варежки и 1 шарф....
1 - Найдите первый челен прогресии (bn) а который b4=1/27; q=1/3...
2
1 / cos(x)^2 - 3 / cos(x) + 2 = 0
так как cos(x) != 0, так как иначе было бы деление на 0, а этого делать нельзя, то умножим обе части уравнения на cos(x)^2. Получаем:
1 - 3cos(x) + 2cos(x)^2 = 0
переставим слагаемые в удобном для нас виде:
2cos(x)^2 - 3cos(x) + 1 = 0
Заметим, что это квадратное уравнение относительно cos(x). Решим его:
D = (-3)^2 - 4 * 2 * 1 = 9 - 8 = 1
cos_1(x) = (-(-3) + sqrt(1)) / (2 * 2) = (3 + 1) / 4 = 4 / 4 = 1
cos_2(x) = (-(-3) - sqrt(1)) / (2 * 2) = (3 - 1) / 4 = 2 / 4 = 1 / 2
cos(x) = 1 при x = 2пn, где n - целое
cos(x) = 1 / 2 при x = п / 4 + 2пk, где k - целое
Наш ответ это совокупность решений для этих двух корней.
ответ: x = 2пn, где n - целое U x = п / 4 + 2пk, где k - целое