Решите уравнение под буквой Е
Другие вопросы по теме Алгебра
Популярные вопросы
- Крышка стола имеет площадь 63 дм2. Его длина равна 9 дм. Чему равна ширина стола?...
2 - Два провідники опорами 2 Ом і 5 Ом, з єднані послідовно, увімкнено до мережі напругою...
2 - Якби ви опинилися в др.пол.19 ст.в Галичині ,то яку політичну партію підтримали?...
2 - Исследуйте на монотонность функцию :1. а) y=б) y=2. а) y=б) y=3. а) y=|x|б) y=-|x|...
3 - фізика 7 клас Завдяки чому існує повітряна оболонка біля поверхні Землі?...
2 - Які речовини належать до стійких органічних забруднювачів...
1 - Решить равенство с числами без знаков...
1 - Как расположен график функции у=кх в зависимости от к ?...
2 - 1.Клетки сетчатки глаза образуются из того же зародышевого листка, что и дерма...
1 - 1.Охарактеризуйте образ побочной партии первой части Пятой симфонии Бетховена....
1
x=(-1±√17)/2
Объяснение:
ОДЗ: x²+x≥0; x²+x+5≥0; 2x²+2x+17≥0⇒x∈(-∞;-1]∪[0;+∞)
(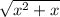 +
+ 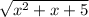 )²=(
)²=(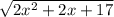 )²
)²
2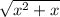
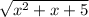 =12
=12
(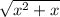
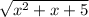 )²=6²
)²=6²
(x²+x)(x²+x+5)=36
x²+x=y⇒x²+x+5=y+5
y(y+5)=36
y²+5y-36=0
y²-4y+9y-36=0
y(y-4)+9(y-4)=0
(y-4)(y+9)=0
1) y-4=0
y=4
x²+x=4
x²+x-4=0
D=1+16=17
x=(-1±√17)/2
(-1+√17)/2>(-1+√16)/2=1,5>0
(-1-√17)/2<(-1-√16)/2=-2,5<-1
2) y+9=0
y=-9
x²+x=-9
x²+x+9=0
D=1-36=-35<0