Решите уравнение log2(x+4)+2log2(1/2-x)=0
Другие вопросы по теме Алгебра
Популярные вопросы
- (7,061/2,3-2,2)*(4,2+17,391/5,27)решите в столбик...
1 - Сочинение-анализ родная деревня . 1)стихотворение,автор, создания.2)тема...
2 - Сделайте таблицу по отечественной войне 1812 г: причины, силы сторон,...
1 - Переведите жазғытұры қалмайды қыстың сызы,масатыдай құлпырар жердің...
2 - Таблица великобритания и ее доминионы...
2 - Дата распада державы александра македонского...
3 - Біографію про дніпрову чайку (бажано своїми словами)...
1 - На память приходит пушкинская строка здесь дух здесь русью пахнет является...
3 - Создать бизнес-план,чтобы в нем были все требования,затраты на материалы,зарплата...
1 - Написать сочинение по на тему трэба праўду шукаць не тапаром, а розумам...
2
Объяснение:
Найдем ОДЗ уравнения , решив систему:
Решим квадратное уравнение :
Учтем ОДЗ.
Значит не принадлежит ОДЗ.
ответ :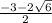 ;0.
;0.