Решите уравнение (кубическое ) x³+x²-1=0
Другие вопросы по теме Алгебра
Популярные вопросы
- қазақ тілі 9тапсырма. Жануарларды табиғаттағы және адам өміріндегі...
3 - Якого за рахунков актора ввів у п’єсу Есхіл...
2 - «Німецьке економічне диво» та Італійське економічне диво НЕ...
2 - Решите уравнение :5 класс стр 142 номер 465...
2 - А(3; -4) В(-5; -2) С(-6; -2) D(-1; -3) Знайти вектор (АВ+СD)...
3 - Выберите один верный ответ Листы в табличном процессоре находились...
3 - 1. В яких агрегатних станах може перебувати водень? ( ) а) Тільки...
1 - . Не могу решить. Тут Два варианта,...
1 - Написать уравнение реакций взаимодействия: а) бутанола с натрием;б)...
3 - 1. Одна из цепочек ДНК имеет последовательность нуклеотидов...
3
Сделаем замену: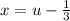 . Подставим:
. Подставим: 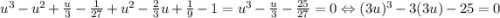 , после замены
, после замены  имеем:
имеем: 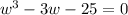 .
.
Пусть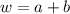 , где
, где 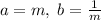 , здесь сразу заметим, что
, здесь сразу заметим, что 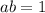 .
.
Подставляем: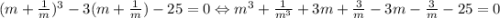 . Далее:
. Далее: 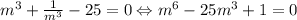 , сделаем очередную замену:
, сделаем очередную замену: 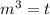 , получим:
, получим: 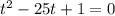 , откуда
, откуда  . Понятно, что
. Понятно, что 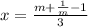
Дальше распутываем клубок замен:![m=\sqrt[3]{\frac{23\pm 5\sqrt{21}}{2}}](/tpl/images/1358/7137/3eca9.png) (сразу заметим, что отрицательный корень не подходит. Это можно обнаружить, исследуя функцию). Итого:
(сразу заметим, что отрицательный корень не подходит. Это можно обнаружить, исследуя функцию). Итого: ![x=\frac{\sqrt[3]{\frac{25+3\sqrt{69}}{2}}+\sqrt[3]{\frac{2}{25+3\sqrt{69}} }-1 }{3}](/tpl/images/1358/7137/d5dcd.png) .
.