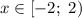Решите уравнение корень из x+2> x
Другие вопросы по теме Алгебра
Популярные вопросы
- Как изменится скорость реакции 2PH3(r)+4O2(r)=P2O5+3H2O при одновременном...
3 - 1.Вычислить значение функции F=(A→B*C)*((A+C)→AB), если А=14,...
3 - даю! Соотнесите утверждения со странами: Англия, Швеция, Пруссия,...
2 - Определите вид, спряжение, образуйте от них деепричастия, выделите...
3 - 6 класс естествование на рисунке изображены создание человека...
3 - На клетчатой бумаге с размером клетки 1х1 изображена трапеция....
2 - 1. в чайнике при комнатной температуре находится 2,5 литра воды....
1 - 1 кг воздуха при температуре 15°С и начальном давлении 1 бар...
3 - Переписать плохим почерком...
2 - Составьте таблицу Перспективы использования богатств Охотского...
2
Рассмотрим два случая:
Решим оба неравенства:
Так как вторая часть неравенства меньше нуля, значит, данное неравенство верно всегда при
Объединим решение этих двух неравенств и найдем их пересечение. Пересечением будет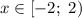
ответ: