Решите уравнение, используя введения новой переменной (2x^2+x-1)(2x^2+x-4)+2=0
RMaGaR
2
26.05.2019 18:10
0
Ответы
vika2499
23.06.2020 06:12
Пускай 2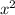
+x=y, тогда (у-1)*(у-4)+2=0, 
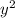-5y+4+2=0, 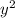-5y+6=0, D=25-4*6=1, y1=(5-1)/2=2, y2=(5+1)/2=3. 2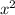+x=2, 2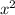+x-2=0, D=1-4*2*(-2)=17, x1=(-1-
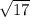)/(2*2)=(-1-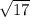)/4, x2=(-1+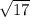)/4. 2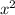+x=3, 2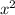+x-3=0, D=1-4*2*(-3)=25, x3=(-1-5)/(2*2)=-1,5, x4=(-1+5)/4=1
ПОКАЗАТЬ ОТВЕТЫ
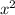+x=y, тогда (у-1)*(у-4)+2=0, 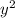-5y+4+2=0, 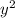-5y+6=0, D=25-4*6=1, y1=(5-1)/2=2, y2=(5+1)/2=3. 2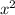+x=2, 2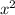+x-2=0, D=1-4*2*(-2)=17, x1=(-1-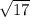)/(2*2)=(-1-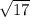)/4, x2=(-1+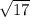)/4. 2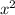+x=3, 2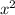+x-3=0, D=1-4*2*(-3)=25, x3=(-1-5)/(2*2)=-1,5, x4=(-1+5)/4=1
Другие вопросы по теме Алгебра
Yuzalina11
09.04.2020 11:36
vadim4ikkek
09.04.2020 11:36
Фарид55
09.04.2020 11:35
ДаРуСя10
09.04.2020 11:35
arturk13
19.04.2020 06:30
Rin1111
19.04.2020 07:21
ruslana0404
19.04.2020 07:15
ЗиА11
19.04.2020 07:15
khsush
19.04.2020 07:14
Популярные вопросы
- Какие варианты предложений можно построить из данных слов? 1. Среди стволов,...
1 - Подготовься записать этот текст по памяти (памятка 5). Дремлет чуткий камыш....
2 - Спиши текст, раскрывая скобки. Божья коровка _ Почему этого жуч(?)ка с яркими...
2 - Обобщи с таблицы, какими основными признаками дает каждый тип текста: повествование,...
3 - Запиши слова в том порядке, в котором они встретятся тебе в словаре. А„етит,...
3 - Представь, что ты редактор Во всех ли предложениях слова употреблены правильно?...
3 - Составь из предложений текст. Употреби глаголы в скобках а форме времени....
2 - Запиши текст, выделяя границы предложений и ставя знаки препинания. Подчеркни...
1 - Подготовься к письму под диктовку (памятка 6). Березовая роща Из всех деревьев...
3 - Прочитай, как и что о своей неожиданной встрече поведала одна школьница....
1