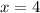1. Алгебра
  2. Решите уравнение используя свойства

Решите уравнение используя свойства функций. √(2х+1)+√(х-3)=4+log1/2 (x-3)

Человечишки Человечишки    3   27.01.2021 23:56    2

Ответы
Nastionka6757 Nastionka6757  27.02.2021 00:23

\sqrt{2x+1}+\sqrt{x-3}=4+\log_{\tfrac{1}{2}}\big(x-3\big)\iff \sqrt{2x+1}+\sqrt{x-3}+\log_{2}(x-3)=4

Рассмотрим функцию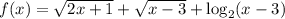 f(x)=\sqrt{2x+1}+\sqrt{x-3}+\log_{2}(x-3) на её области определения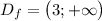 D_{f}=\big(3;+\infty\big)

График этой функции пересечёт линию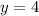 y=4 более одного раза только если будут существовать промежутки разной монотонности (на каких-то функция возрастает, на других - убывает).

Обязательным условием смены монотонности функции является обращение её производной в ноль (или несуществование производной) в точке, где монотонность меняется. Попробуем их найти.

f'(x)=\dfrac{1}{\sqrt{2x+1}}+\dfrac{1}{2\sqrt{x-3}}+\dfrac{1}{(x-3)\ln 2} 0~\big(\forall x\in D_{f}\big)

Как видно из вида производной, для всех точек области определения функции, она не обращается в ноль (более того, функция строго возрастает).

Таким образом, наше уравнение не может иметь более одного корня.

Методом пристального взгляда замечаем, что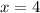 x=4 - корень уравнения.

Действительно,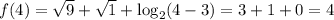 f(4)=\sqrt{9}+\sqrt{1}+\log_{2}(4-3)=3+1+0=4

ответ. x=4

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Dantebayo Dantebayo  14.09.2019 13:40
Сколько корней имеет уравнение x^7=-1...
Fazi8833 Fazi8833  14.09.2019 13:40
Вычислите: корень 5 степени -1/243 - корень 4 степени 625/16...
jcyueurur jcyueurur  14.09.2019 13:40
Решить пример, не могу понять как к общему корню или что-то вроде этого 5√6 + 4√24 - 3√2...
musiclove2 musiclove2  14.09.2019 13:40
Нужна : вынесите множитель под знак корня: а) 4√5= б) -5√6= в) 1/8√48= г) 2/5√35=...
джанил джанил  14.09.2019 13:40
Решите не строя графика функции, записать точку пересечения графика с осью oy, и выяснить, является функция убывающей или возрастающей....
yulia3789 yulia3789  14.09.2019 13:40
Трудно ли сдавать огэ, если не знаешь таблицы умножения?...
Lqoki11 Lqoki11  22.07.2019 10:40
Найдите наименьшее значение многочлена p(x)=x²+10x+1...
glebshestopal glebshestopal  22.07.2019 10:40
Найдите tg α если (2 sin α + cos α +1)/(4 sin α + 2 cos α + 3)=1/3...
Иван55551 Иван55551  22.07.2019 10:40
Дано уравнение: (x−a)(x2−8x+7)=0 найди те значения a, при которых уравнение имеет три разных корня, и они образуют арифметическую прогрессию. вводи возможные значения a...
kuznitsovas kuznitsovas  22.07.2019 10:40
Есть 4 карточки с цифрами 1, 2, 3 и 4. сколько различных трёхзначных чисел, делящихся на 6, можно составить из этих карточек? цифры в записи числа не должны повторяться...

Популярные вопросы