Решите уравнение. (х-2)в 4 степени минус (х-2) во 2 степени минус 6=0
Другие вопросы по теме Алгебра
Популярные вопросы
- Разложите на множители100-Ba+5)2 даю 20б...
2 - составить кластер на тему Наурыз...
3 - 10 г алюмінію спалили.Який об єм кисню витрачено,яка кількість...
1 - Выберете верныйсуждение запешыте цфры под которами они указоны...
2 - ,мне через 30 минут сдавать...
2 - USE OF ENGLISH Complete the sentences with affirmative and negative...
1 - Задание 2. Письменно проанализируйте сказку М.Е. Салтыкова-Щедрина...
3 - 1. Что будет выведено на экран в результате выполнения инструкции...
3 - Декорирование изделия. Организация выставки дайте ответы...
3 - План до твору 25-ий розділ Тореадори з Васюківки....
1
(x - 2)⁴ - (x - 2)² - 6 = 0
(x - 2)² = t - новая переменная
(x - 2)² = 3 или (x - 2)² = -2
x² - 4x + 4 - 3 = 0 корней нет
x² - 4x + 1 = 0
D = (-4)² - 4 * 1 * 1 = 16 - 4 = 12
ответ: 2 ± √3
Объяснение:
Пусть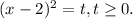 Тогда уравнение принимает вид:
Тогда уравнение принимает вид:
Условию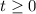 удовлетворяет t=3. Значит
удовлетворяет t=3. Значит