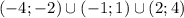Решите уравнение х^2-3|х|+2/|х|-4 < 0
Другие вопросы по теме Алгебра
Популярные вопросы
- Найти работу выхода электронов с поверхности меди, которую облучают...
3 - Найдите площадь полной поверхности правильной н-угольной пирамиды...
2 - Даны координаты трех вершин прямоугольника ABCD: А (–1;–3), С(5;...
2 - Дано точки A ( -5 ; 3 ) , В ( 0 ; -6 ) , С ( 3 ; 7 ) , D (4 ; 0...
1 - Зробити ланцюг живлення з словами Морква- Пшениця-...
2 - Прочитайте. Спишите предложения с однороднымичленами. Подчеркните...
2 - Придумайте ситуацию в которой нарушаются сразу несколько отраслей...
1 - Кто мне если я им сделаю лучший ответ, 5 звездочек Если сделать...
2 - Сочинение на тему без исторических памятников нет жизни...
1 - Заполнить таблицу Используя фрагмент уч фильма ссылка https://ru.savefrom.net/7/#url=http://youtube.com/watch?v=C0k0iiuSY3U&utm_source=youtube.com&utm_medium=short_domains&utm_campaign=www.ssyoutube.com&a_ts=1585148045.539...
1
Домножим неравенство на положительное выражение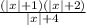
Получаем
Дальше применяется стандартный метод интервалов: рисуются на числовой прямой нули числителя и знаменателя и расставляются знаки. Поскольку Ваша задача достаточно продвинутая, я делаю вывод, что учить Вас методу интервалов не надо.
ответ: