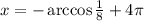Решите уравнение cos4x - cosx = 0 и укажите количество корней из промежудка [0; 4пи].
Другие вопросы по теме Алгебра
Популярные вопросы
- Мне нравится море с большими красивыми волнами.поставить знаки препинания....
3 - Подготовьте краткое сообщение о финикийских мореплавателях...
2 - Почему в сказке кладовая солнца пришвина настю называли золотая...
1 - Ширина коробки конфет 2дм ,а длина на 2дм.больше найди площадь коробки...
2 - А1. процесс приобретения знаний о мире: 1) культура 3) труд 2) мораль...
3 - 45 разделить на 14 деление с остатком...
1 - Морфемный и словообразовательный разбор слова мировой и приободрить...
3 - Вы все еще гуляете? воскликнула маленькая полина увидев леву с мамой...
3 - Объясните понятие восточный вопрос...
3 - Запиши слова в 3 ряда: 1) слово в которых больше букв, чем звуков...
3
Пусть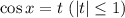 , получим квадратное уравнение относительно t:
, получим квадратное уравнение относительно t:
Возвращаемся к обратной замене
Отбор корней из промежутка принадлежащих [0;4π]:
1. Для корня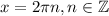
Если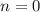 то
то 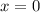
Если то
то 
Если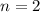 то
то 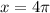
2. Для корня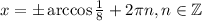
Если n=0, то
Если n=1, то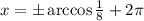
Если n=2, то