Решите уравнение: cos2x+sinx=cos^2x. укажите корни, принадлежащие отрезку [0; 2π]
Другие вопросы по теме Алгебра
Популярные вопросы
- Спешите слова разделите их для переноса поставте ударение.газ, тряти, плод, флейта,...
2 - А^2 -2a +6 нужно собрать квадрат разности,...
3 - Морфемный разбор слова написала !...
3 - Прислывя козакові без як дівчені без намиста...
2 - Вынесите множитель из под знака корня корень 18 корень 40 корень 50 корень 48...
3 - Найдите лишние слова в каждой группе.спиши остальные слова,обозначь суффиксы. 1)...
1 - Для нумерации страниц учебника понадобилось 366 цифр. нумерация начинается с первой...
2 - Какова длина отрезка изображающая расстояние на местности 1 км,на карте,если масштаб...
1 - 8класс электричество.для зажигания лампы используется электроёмкость конденсатора...
3 - Мені потрібно твір сімя голованчиків...
3
Объяснение:
Выберем корни, принадлежащие отрезку [ 0; 2π]
1) при n=0, x=0;
при n=1, x=π;
при n=2, x=2π.
2) при k=0, x=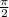 .
.