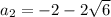Решите уравнение a^4+8a^3+8a^2-32a-240=0
Другие вопросы по теме Алгебра
Популярные вопросы
- Найдите tg2a если sina=-0.8 и p...
2 - Изучите состав некоторых лекарственных средств из вашей аптечки. Посмотрите информацию...
2 - решить задачу с оформлением...
1 - Вертикальный шест, одна задача....
3 - ответ Персонаж A Ырыскельды Б Бабушка Ботая 3. Установите соответствие: Высказывание...
3 - решить задачу с оформлением...
2 - правильные варианты. Вопрос: особенности миног и миксин 1.хорда на протяжении всех...
1 - Какое поручение было дано братьям строгановым?...
2 - 1954-1964 жыл Жылымық деп аталу себебі неде?...
2 - Сложный эфир X подвергли кислотному гидролизу и получили соединения Y и Z. Если...
3
файл
произведём замену переменных
Cчитаем дискриминант:
Дискриминант положительный
Уравнение имеет два различных корня:
исходное уравнение сводится к уравнению
================================================
Случай 1
Cчитаем дискриминант:
Дискриминант отрицательный, следовательно уравнение не имеет действительных решений
=================================================
Случай 2
Cчитаем дискриминант:
Дискриминант положительный
Уравнение имеет два различных корня:
ответ: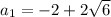 ;
;