Решите уравнение A^2x+1=20
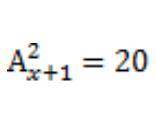
Другие вопросы по теме Алгебра
Популярные вопросы
- Преобразуйте выражение в многочлен стандартного вида а) 2а(2-b) б) (2а-3b)(3b-2а)...
3 - Тест по теме «многоликий восток» 1. соотнесите название страны и титул ее...
2 - Моя уявна подорож стародавнім вавілоном....
3 - 3) if you are hungry, you have some pizza.a) mustn tb) couldc) should4)...
3 - Известные газеты в россии в 19 веке...
2 - Матан! выбрать правильный вариант ответа линейное уравнение...
2 - Дівчатка поділили одне й те саме число: софійка — на 4, атетянка — на 8....
1 - Поставьте слова в правильную форму this soup is (taste) it needs more salt...
3 - Человек стоит от уличного фонаря на расстоянии 8м.при этом длина тени равна...
2 - Запишите |x| если а)x=12 б)x=-7 в...
1
Шаг 1: Выразите x.
Для этого вычтем 1 из обеих сторон уравнения:
A^2x = 20 - 1
A^2x = 19
Шаг 2: Избавьтесь от степени A.
Чтобы избавиться от степени A, применим логарифмическую функцию к обоим сторонам уравнения. В данном случае мы можем использовать натуральный логарифм, обозначенный как ln.
ln(A^2x) = ln(19)
Шаг 3: Примените свойство логарифмов.
По свойству логарифмов ln(A^2x) = (2x)ln(A). Используя это свойство, мы можем преобразовать уравнение:
(2x)ln(A) = ln(19)
Шаг 4: Выразите x.
Чтобы выразить x, разделим обе стороны уравнения на 2ln(A):
2x = ln(19)/(ln(A))
Шаг 5: Разделите на 2.
Чтобы получить x, разделим обе стороны уравнения на 2:
x = ln(19)/(2ln(A))
Таким образом, решение уравнения A^2x+1=20 представляется в виде x = ln(19)/(2ln(A)).
При решении данного уравнения будет необходимо знание логарифмических функций и их свойств.