Решите уравнение: 6sin^2x+5cosx-5=0
Другие вопросы по теме Алгебра
Популярные вопросы
- Соченение сообшение последний листок ...
1 - Екі мәтінді салыстыр. Тақырыбы:1-мәтін 2-мәтін1)Ұқсастығы:2)Айырмашылығы:3)...
2 - Выпиши предложение, в котором необходимо поставить одну запятую. Расставь...
1 - С МЕНЯ ‼️‼️‼️‼️‼️‼️ Відрізок DA -- перпендикуляр до площини трикутника ABC,AB...
1 - Лабораторная работа номер 3. Сделайте...
2 - Оцените периметр и площадь прямоугольника со сторонами а см и b см, где...
3 - Тест. Умножение положительных и отрицательных чиселВариант 1Часть АА 1....
3 - Место образования половых клеток у споровых растений...
1 - Характеристика Васи или его отца в рассказе «В дурном обществе» до 18:00...
2 - 2-тапсырма. І нұсқа: «Тәуелсіздікті аңсаған тарландар» эссе жазыңыз(желательно...
2
Объяснение:
Пусть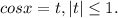 Тогда уравнение принимает вид:
Тогда уравнение принимает вид:
Возвращаемся к замене :