Решите уравнение :5√x^3+4x^2-2=5√x^2+4x-2
Другие вопросы по теме Алгебра
Популярные вопросы
- Упредставителей каких царств в клетках имеются лизосомы,пероксимы,пластиды,эндоплазматическая...
1 - Перебудуйте речення з прямою мовою в речення з непрямою мовою....
2 - Составить из цифр правильный айпи адрес a) 3212 б )21 в)2.12 г)4...
2 - Объясните грамматику present perfect подробно и напишите примеры...
1 - H=190 cм m=1 кг t= 1/100 c найти f взаимодействия...
2 - Как ребенку объяснить что такое обратная ?...
1 - Ниже ряд терминов. все они , за исключением двух , относятся к...
3 - Решите : 1) 2cos(x/3-π/3)=√3 2) cos(π/2+2x)=1 3) sin(2x-π/4)=0...
3 - Почему горящее дерево излучает тепло?...
1 - Дано прогресію (сn) з додатніми числами , у чкій с4= 24,с6= 96.скільки...
2
Сделаем вид, что оба корня существуют, возведем обе части в квадрат, найдем корни, а потом проверим их прямой подстановкой.
Возводим в квадрат:
Отсюда получаем три корня: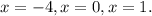
Подставим их в исходное уравнение (разделенное на 5 для удобства):
Да, под корнем одинаковые числа. Однако, так как корень из отрицательного числа не определен на множестве действительных чисел, х = -4 не является корнем уравнения.
Аналогичная ситуация. х = 0 не является корнем уравнения.
ОТВЕТ: {1}.