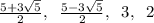Решите уравнение: 1) x=32+2√x+3 2) (x²-5x+2)(x²-5x-1)=28
Другие вопросы по теме Алгебра
Популярные вопросы
- 15 минут осталось решить >...
1 - составьте разветвляющие алгоритмы пословиц1. Без друга в жизни туго2....
2 - По 431A. Прочитай тексты. Определи тип и стиль речи.солнцем. Но под...
3 - T у подножия горы -6°Сt на вершине горы 16°CНайти h горы...
2 - ЗАДАНИЯ 1. Выделите на карте границы океанов иПодпишите их названия.2....
1 - Дан куб ABCDA1B1C1D1; A1B1 = 6 см, B1C1 = 6 см, AA1= 10 см, точка...
2 - с грамматикой по английскому,напишите ответ цифроми и буквами...
1 - Составьте предложения по схемам ...
3 - Во сколько раз 1 ц больше 50 кг ...
3 - Пронализируйте этапы образования мочи...
3
Оба уравнения решаются с замены
В первом уравнении мы ввели замену t = √x
Во втором уравнении t = x²-5x+2
ответ: 49
ответ: